题目内容
3.用数学归纳法证明:$\frac{1}{\sqrt{1×2}}+\frac{1}{\sqrt{2×3}}+…+\frac{1}{\sqrt{n(n+1)}}$$<\sqrt{n}$(n∈N*).分析 利用数学归纳法证明即可,注意在证明n=k+1时利用不等式$\frac{1}{\sqrt{(k+1)(k+2)}}$<$\frac{1}{\sqrt{k(k+1)}}$放缩.
解答 证明:(1)当n=1时,左边=$\frac{1}{\sqrt{2}}$<1=右边;
(2)假设当n=k(k∈N*)时,$\frac{1}{\sqrt{1×2}}$+$\frac{1}{\sqrt{2×3}}$+…+$\frac{1}{\sqrt{k(k+1)}}$$<\sqrt{k}$成立.
则当n=k+1时,左边=$\frac{1}{\sqrt{1×2}}$+$\frac{1}{\sqrt{2×3}}$+…+$\frac{1}{\sqrt{k(k+1)}}$+$\frac{1}{\sqrt{(k+1)(k+2)}}$$<\sqrt{k}$+$\frac{1}{\sqrt{(k+1)(k+2)}}$<$\sqrt{k}$+$\frac{1}{\sqrt{k(k+1)}}$=$\sqrt{k}$+$(\sqrt{k+1}-\sqrt{k})$=$\sqrt{k+1}$=右边.
∴当n=k+1时,不等式成立.
综上可得:?n∈N*,$\frac{1}{\sqrt{1×2}}+\frac{1}{\sqrt{2×3}}+…+\frac{1}{\sqrt{n(n+1)}}$$<\sqrt{n}$成立.
点评 本题考查了数学归纳法证明不等式、不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
13.设不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ y≤-kx+4k\end{array}\right.$在平面直角坐标系中所表示的区域的面积为S,则当k>1时,$\frac{kS}{k-1}$的最小值为( )
| A. | 16 | B. | 32 | C. | 48 | D. | 56 |
11.下列图形均表示两个相交平面,其中画法正确的是( )
| A. | 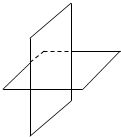 | B. | 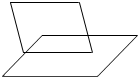 | C. | 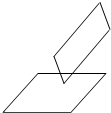 | D. |  |