题目内容
在 中,
中, 分别为角
分别为角 所对的边,且
所对的边,且 ,
, ,
, ,求角
,求角 的正弦值.
的正弦值.
 .
.
解析试题分析:由 的结构特点可联想到两角和的正切公式,求出
的结构特点可联想到两角和的正切公式,求出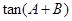 后,再根据三角形内角和定理,可求出角
后,再根据三角形内角和定理,可求出角 ,再由余弦定理,结合题目中边的长度关系解方程组,便可得到各边长度,由正弦定理可求出角
,再由余弦定理,结合题目中边的长度关系解方程组,便可得到各边长度,由正弦定理可求出角 的正弦值.解决三角形问题时,一般可通过正弦定理和余弦定理沟通三角形的边角关系,还要注意方程的思想的应用.
的正弦值.解决三角形问题时,一般可通过正弦定理和余弦定理沟通三角形的边角关系,还要注意方程的思想的应用.
试题解析:由 ,知
,知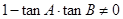 .(否则
.(否则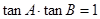 ,则
,则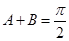 ,但由
,但由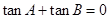 ,知
,知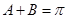 ,矛盾)
,矛盾)
故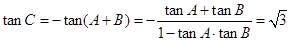 ,所以
,所以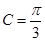 5分
5分
由余弦定理得,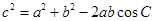 即
即 ,得
,得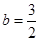 ,所以
,所以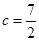 ,
,
由正弦定理得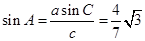 12分
12分
考点:三角函数公式的应用、正弦定理、余弦定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,
, ,
, 分别是角
分别是角 ,
, ,
, 的对边,向量
的对边,向量 ,
, ,且
,且 //
// .
. 的大小;
的大小; ,且
,且 的最小正周期为
的最小正周期为 ,求
,求 上的最大值和最小值.
上的最大值和最小值.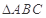 中,已知角
中,已知角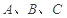 的对边分别为
的对边分别为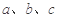 .向量
.向量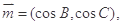
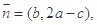 且向量
且向量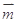 与
与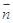 共线.
共线.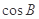 的值;
的值;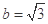 ,求
,求 中,已知
中,已知
 ;
; ,
, ,求
,求 .
. 中,已知
中,已知 .
. 的值;
的值; ,
, ,求
,求 .
. 中,
中, 边上的中线
边上的中线 长为3,且
长为3,且 ,
, .
.
 的值;(Ⅱ)求
的值;(Ⅱ)求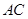 边的长.
边的长. 中,
中, 、
、 、
、 分别是三内角
分别是三内角 、
、 、
、 的对边,已知
的对边,已知 .
. ,判断
,判断 中,内角
中,内角 的对边分别为
的对边分别为 ,已知
,已知 .
. ;
; ,求△
,求△ ,求
,求 的取值范围.
的取值范围.