题目内容
设f(x)为定义在R上的偶函数,当x≤-1时,y=f(x)的图象是经过点(-2,0)、斜率为1的射线;又在y=f(x)的图象中有一部分是顶点在(0,2),且过点(-1,1)的一段抛物线.求函数f(x)的解析式,画出流程图,并编写一个程序,对每一个输入的x值,求出相应的函数值.
思路分析:本题考查函数的解析式的求法及条件结构的程序框图的设计.
由题意可知y=x+2(x≤-1),因为f(x)在R上是偶函数,
所以y=-x+2(x≥1),
又由于f(x)的图象是抛物线的一部分,顶点为(0,2).
故![]() =0,即b=0;
=0,即b=0;![]() =2,即c=2.
=2,即c=2.
又因为过点(-1,1),故有a=-1.
又因为f(x)为偶函数,故f(x)=-x2+2(-1<x<1).
解:f(x)=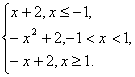
程序框图如图1-2-7所示.
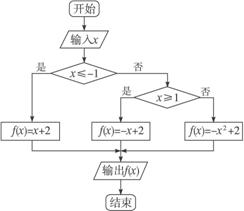
图1-2-7
程序步骤如下:
INPUT x
IF x<=-1 THEN
PRINT x+2
ELSE
IF x>=1 THEN
PRINT -x+2
ELSE
PRINT -x^2+2
END IF
END IF
END
方法归纳 由于函数f(x)的解析式是一个分段函数,所以输入x的值后,应根据x的值所在的范围选择相应的解析式代入求出其函数值,故应用条件语句.又因为实数x的值共分为三个范围,所以还应用到条件语句的嵌套.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
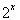
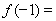
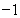
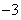
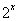
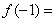
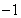
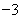
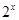 +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=