题目内容
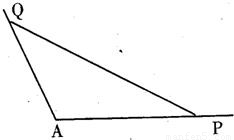
如图所示,角A为钝角,且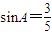 ,点P、Q分别在角A的两边上.
,点P、Q分别在角A的两边上.(1)AP=5,PQ=
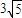 ,求AQ的长;
,求AQ的长;(2)设
 的值.
的值.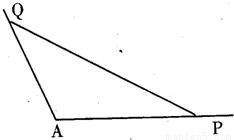
【答案】分析:(1)由A为钝角,利用同角三角函数间的基本关系求出cosA的值,然后利用余弦定理得到关于AQ的方程,求出方程的解即可得到满足题意的AQ的长;
(2)由cosα的值利用同角三角函数间的基本关系求出sinα的值,根据三角形的内角和定理及诱导公式求出sinA的值及cosA的值,然后把2α+β变为α+(α+β),利用两角和的正弦函数公式化简后,分别将各自的值代入即可求出所求式子的值.
解答:解:(1)∵∠A是钝角,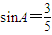 ,∴
,∴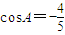 ,
,
在△APQ中,PQ2=AP2+AQ2-2AP•AQcosA,
∴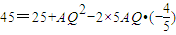 ,
,
解得AQ=2或AQ=-10(舍)即AQ=2;
(2)由cosα=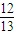 ,得sinα=
,得sinα=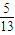 ,
,
又sin(α+β)=sinA=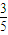 ,cos(α+β)=-cosA=
,cos(α+β)=-cosA=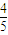 ,
,
∴sin(2α+β)=sin[α+(α+β)]=sinαcos(α+β)+cosαsin(α+β)=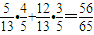 .
.
点评:此题要求学生灵活运用余弦定理化简求值,掌握三角形的内角和定理,灵活运用两角和的正弦函数公式及同角三角函数间的基本关系化简求值,是一道综合题.
(2)由cosα的值利用同角三角函数间的基本关系求出sinα的值,根据三角形的内角和定理及诱导公式求出sinA的值及cosA的值,然后把2α+β变为α+(α+β),利用两角和的正弦函数公式化简后,分别将各自的值代入即可求出所求式子的值.
解答:解:(1)∵∠A是钝角,
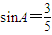 ,∴
,∴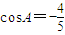 ,
,在△APQ中,PQ2=AP2+AQ2-2AP•AQcosA,
∴
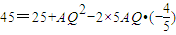 ,
,解得AQ=2或AQ=-10(舍)即AQ=2;
(2)由cosα=
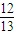 ,得sinα=
,得sinα=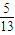 ,
,又sin(α+β)=sinA=
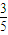 ,cos(α+β)=-cosA=
,cos(α+β)=-cosA=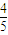 ,
,∴sin(2α+β)=sin[α+(α+β)]=sinαcos(α+β)+cosαsin(α+β)=
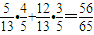 .
.点评:此题要求学生灵活运用余弦定理化简求值,掌握三角形的内角和定理,灵活运用两角和的正弦函数公式及同角三角函数间的基本关系化简求值,是一道综合题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
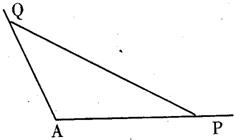 如图所示,角A为钝角,且sinA=
如图所示,角A为钝角,且sinA= (2013•茂名一模)如图所示,角A为钝角,且
(2013•茂名一模)如图所示,角A为钝角,且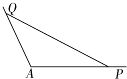 如图所示,角A为钝角,且sinA=
如图所示,角A为钝角,且sinA=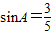 ,点P、Q分别在角A的两边上.
,点P、Q分别在角A的两边上.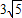 ,求AQ的长;
,求AQ的长; 的值.
的值.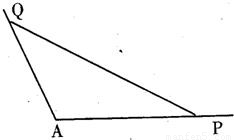
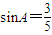 ,点P、Q分别在角A的两边上.
,点P、Q分别在角A的两边上.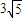 ,求AQ的长;
,求AQ的长; 的值.
的值.