��Ŀ����
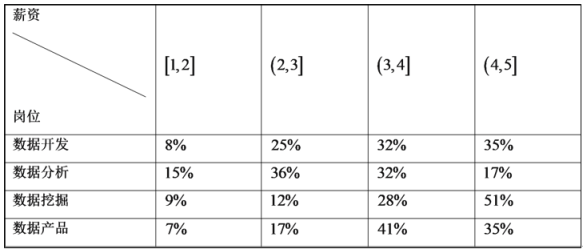
����Ŀ��ij���ڴ�����ȫ�����������������Ĺ����У�Ϊ�˵�������Դ�����ȫ�����������������������˽������������һ��֪ʶ�ʾ����飨һλ����ֻ�ܲμ�һ�Σ���ͨ������������õ��μ��ʾ������1000�˵ĵ÷֣�����100�֣�ͳ�ƽ�����±���ʾ��
��� |
|
|
|
|
|
|
|
Ƶ�� | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
��1�����аѵ÷ֲ�����80�ֵ������Ϊ������������������Ƶ�ʹ��Ƹ��ʣ��������������壬��Ӹ��е������������ȡһλ���鵽�������������ĸ��ʣ�
��2����Ƶ���ֲ������Դ�����Ϊ���˴��ʾ�����ĵ÷�![]() ������̬�ֲ�
������̬�ֲ�![]() ��
��![]() ����Ϊ��1000�˵÷ֵ�ƽ��ֵ��ͬһ�������ø�������������е�ֵ��ʾ����������̬�ֲ���֪ʶ��
����Ϊ��1000�˵÷ֵ�ƽ��ֵ��ͬһ�������ø�������������е�ֵ��ʾ����������̬�ֲ���֪ʶ��![]() ��
��
��3���ڣ�2���������£�����Ϊ�˴βμ��ʾ�����������ƶ����½���������
�������÷ֲ�����![]() �Ŀ��Ի���2��������ѣ��÷ֵ���
�Ŀ��Ի���2��������ѣ��÷ֵ���![]() �Ŀ��Ի���1��������ѣ�
�Ŀ��Ի���1��������ѣ�
������ÿ�λ����͵�������ѺͶ�Ӧ�ĸ���Ϊ��
���͵�������ѣ���Ԫ��Ԫ�� | 30 | 60 |
���� | 0.75 | 0.25 |
���������Ҫ�μӴ˴��ʾ����飬��![]() ����λ��Ԫ��Ϊ������μ��ʾ���������Ļ��ѣ���
����λ��Ԫ��Ϊ������μ��ʾ���������Ļ��ѣ���![]() �ķֲ�������ѧ������
�ķֲ�������ѧ������
�����ο������빫ʽ
![]() ����
����![]() �����
�����![]() ��
��
��![]() ����
����![]() ��
��
���𰸡���1��![]() ����2��
����2��![]() ����3���ֲ��м�������
����3���ֲ��м�������![]()
��������
��1���ɹŵ�����ʹ�ʽֱ�Ӽ���õ������
��2������Ƶ���ֲ����ɼ���õ�![]() ���ɴ�ȷ��
���ɴ�ȷ��![]() ��������̬�ֲ����ߵ����ʿ���ý����
��������̬�ֲ����ߵ����ʿ���ý����
��3������ȷ��![]() ���п��ܵ�ȡֵ�����ݶ����¼����ʹ�ʽ�����ÿ��ȡֵ��Ӧ�ĸ��ʣ��ɴ˵õ��ֲ��У�������ѧ�������㹫ʽ�������ѧ����.
���п��ܵ�ȡֵ�����ݶ����¼����ʹ�ʽ�����ÿ��ȡֵ��Ӧ�ĸ��ʣ��ɴ˵õ��ֲ��У�������ѧ�������㹫ʽ�������ѧ����.
��1����Ӹ��е������������ȡһλ���鵽������������Ϊ�¼�![]() ��
��
��![]() ��
��
��2��![]()
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��3��������֪��![]() ��
��![]() ��
��
![]() �Ŀ���ȡֵΪ
�Ŀ���ȡֵΪ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
�� ��
��
![]() ��
��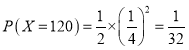 ��
��
��![]() �ķֲ���Ϊ��
�ķֲ���Ϊ��
|
|
|
|
|
|
|
|
|
|
![]() .
.