题目内容
8.已知函数f(x)=ax(a>0,a≠1),其导函数为f′(x),满足f(x)<f′(x)对于任意实数x恒成立,则( )| A. | f(1)>e,f(2012)>e2012 | B. | f(1)>e,f(2012)<e2012 | ||
| C. | f(1)<e,f(2012)>e2012 | D. | f(1)<e,f(2012)<e2012 |
分析 构造函数g(x)=$\frac{f(x)}{{e}^{x}}$,求导g′(x)=$\frac{f′(x){e}^{x}-f(x){e}^{x}}{({e}^{x})^{2}}$=$\frac{f′(x)-f(x)}{{e}^{x}}$,从而可得a>e,从而解得.
解答 解:令g(x)=$\frac{f(x)}{{e}^{x}}$,故g′(x)=$\frac{f′(x){e}^{x}-f(x){e}^{x}}{({e}^{x})^{2}}$=$\frac{f′(x)-f(x)}{{e}^{x}}$,
∵f(x)<f′(x)对于任意实数x恒成立,
∴g′(x)>0对于任意实数x恒成立,
∴g(x)=$\frac{f(x)}{{e}^{x}}$=$(\frac{a}{e})^{x}$在R上是增函数,
故$\frac{a}{e}$>1,即a>e,
∴f(1)=a>e,f(2012)=a2012>e2012,
故选:A.
点评 本题考查了导数的综合应用,关键在于构造函数g(x)=$\frac{f(x)}{{e}^{x}}$.

练习册系列答案
相关题目
16.设α∈R,函数f(x)=($\frac{1}{3}$)x-1-a的图象一定经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
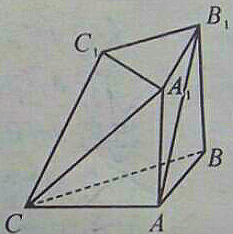 如图在多面体ABC-A1B1C1中,AA1$\underset{∥}{=}$BB1,B1C1$\underset{∥}{=}$$\frac{1}{2}$BC,求证:AB1∥平面 A1C1C.
如图在多面体ABC-A1B1C1中,AA1$\underset{∥}{=}$BB1,B1C1$\underset{∥}{=}$$\frac{1}{2}$BC,求证:AB1∥平面 A1C1C.