题目内容

F1，F2分别为椭圆
x2
2
+y2=1的左右焦点，点P（x，y）在直线x+y-2=0上（x≠2且x≠±1），直线PF1，PF2的斜率分别为k1、k2，则
1
k1
-
3
k2
的值为（　　）
分析：先确定椭圆的左右焦点坐标，再表示出斜率，进而计算
1
k1
-
3
k2
，利用点P（x，y）在直线x+y-2=0上（x≠2且x≠±1），即可求得结论．
解答：解：由题意，F1（-1，0），F2（1，0）
∵直线PF1，PF2的斜率分别为k1、k2，
∴
1
k1
-
3
k2
=
x+1
y
-
3(x-1)
y
=
-2x+4
y

∵点P（x，y）在直线x+y-2=0上（x≠2且x≠±1），
∴y=2-x，∴
-2x+4
y
=2
∴
1
k1
-
3
k2
=2
故选A．
点评：本题考查椭圆的几何性质，考查斜率的计算，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
1
2
，F1、F2分别为椭圆C的左、右焦点，若椭圆C的焦距为2．
（1）求椭圆C的方程；
（2）设M为椭圆上任意一点，以M为圆心，MF1为半径作圆M，当圆M与直线l：x=
a2
c
有公共点时，求△MF1F2面积的最大值．
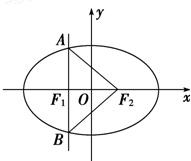精英家教网已知F1，F2分别为椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左，右焦点，过F1且垂直于x轴的直线交椭圆C于A，B两点，若△ABF2为钝角三角形，则椭圆C的离心率e的取值范围为（　　）
A、（0，
2
-1）
B、（0，
3
-1）
C、（
2
-1，1）
D、（
3
-1，1）
设F1，F2分别为椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的左、右两个焦点，若椭圆C上的点A（1，
3
2
）到F1，F2两点的距离之和等于4．
（1）写出椭圆C的方程和焦点坐标；
（2）过点P（1，
1
4
）的直线与椭圆交于两点D、E，若DP=PE，求直线DE的方程；
（3）过点Q（1，0）的直线与椭圆交于两点M、N，若△OMN面积取得最大，求直线MN的方程．
（2012•鹰潭一模）已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)．F1，F2分别为椭圆C的左，右焦点，A1，A2分别为椭圆C的左，右顶点．过右焦点F2且垂直于x轴的直线与椭圆C在第一象限的交点为M(
3
，2)．
（1）求椭圆C的标准方程；
（2）直线l：x=my+1与椭圆C交于P，Q两点，直线A1P与A2Q交于点S．当直线l变化时，点S是否恒在一条定直线上？若是，求此定直线方程；若不是，请说明理由．
（2007•杨浦区二模）（文）设F1、F2分别为椭圆C：
x2
m2
+
y2
n2
=1（m＞0，n＞0且m≠n）的两个焦点．
（1）若椭圆C上的点A（1，
3
2
）到两个焦点的距离之和等于4，求椭圆C的方程．
（2）如果点P是（1）中所得椭圆上的任意一点，且
PF1
•
PF2
=0，求△PF1F2的面积．
（3）若椭圆C具有如下性质：设M、N是椭圆C上关于原点对称的两点，点Q是椭圆上任意一点，且直线QM与直线QN的斜率都存在，分别记为KQM、KQN，那么KQM和KQN之积是与点Q位置无关的定值．试问：双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）是否具有类似的性质？并证明你的结论．通过对上面问题进一步研究，请你概括具有上述性质的二次曲线更为一般的结论，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网