题目内容
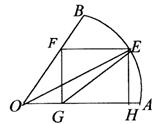
扇形AOB的中心角为2θ,半径为r,在扇形AOB中作内切圆O1及与圆O1外切,与OA,OB相切的圆O2,问sinθ为何值时,圆O2的面积最大?最大值是多少?
解:设圆O1及与圆O2的半径分别为r1,r2,
则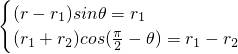 ,得
,得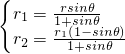 ,
,
∴ ,
,
∵0<2θ<2π,∴0<θ<π,令t=sinθ+1(1<t<2),
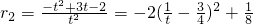 ,当
,当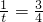 ,即
,即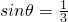 时,
时,
圆O2的半径最大,圆O2的面积最大,最大面积为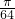 .
.
分析:运用圆与圆的位置关系和圆的面积公式进行求解.
点评:正确掌握圆与圆的位置关系是准确解题的关键.
则
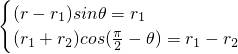 ,得
,得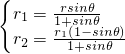 ,
,∴
 ,
,∵0<2θ<2π,∴0<θ<π,令t=sinθ+1(1<t<2),
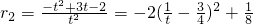 ,当
,当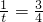 ,即
,即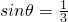 时,
时,圆O2的半径最大,圆O2的面积最大,最大面积为
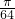 .
.分析:运用圆与圆的位置关系和圆的面积公式进行求解.
点评:正确掌握圆与圆的位置关系是准确解题的关键.

练习册系列答案
相关题目