题目内容
有以下4个结论:①若sinα+cosα=1,那么sinnα+cosnα=1; ②x=
π是函数y=sin (2x+
π)的一条对称轴; ③y=cosx,x∈R在第四象限是增函数; ④函数y=sin (
π+x)是偶函数; 其中正确结论的序号是______.
| 1 |
| 8 |
| 5 |
| 4 |
| 3 |
| 2 |
对于①由sinα+cosα=1知,
或
,从而有sinnα+cosnα=1;故①的结论正确;
②验证当x=
π时,函数y=sin (2x+
π)=sin (2×
+
π)=sin
=- 1,所以x=
π是函数y=sin (2x+
π)的一条对称轴,②的结论正确;
③举反例如:设x1=-
,x2=
均是第四象限的角,且x1<x2,但是cosx1=cosx2=
所以y=cosx,x∈R在第四象限是增函数,此结论错误;
④函数y=sin (
π+x)=-cosx,显然这是一个偶函数,结论正确.
故答案为:①②④.
|
|
②验证当x=
| 1 |
| 8 |
| 5 |
| 4 |
| π |
| 8 |
| 5 |
| 4 |
| 3π |
| 2 |
| 1 |
| 8 |
| 5 |
| 4 |
③举反例如:设x1=-
| π |
| 4 |
| 7π |
| 4 |
| ||
| 2 |
④函数y=sin (
| 3 |
| 2 |
故答案为:①②④.

练习册系列答案
相关题目
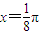 是函数
是函数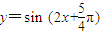 的一条对称轴; ③y=cosx,x∈R在第四象限是增函数; ④函数
的一条对称轴; ③y=cosx,x∈R在第四象限是增函数; ④函数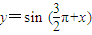 是偶函数; 其中正确结论的序号是 .
是偶函数; 其中正确结论的序号是 .