题目内容
近几年来,我国许多地区经常出现干旱现象,为抗旱经常要进行人工降雨。现由天气预报得知,某地在未来3天的指定时间的降雨概率是:前2天均为50%,后1天为80%.3天内任何一天的该指定时间没有降雨,则在当天实行人工降雨,否则,当天不实施人工降雨.求不需要人工降雨的天数x的分布列和期望.
x分布列是
期望是1.8 x 0 1 2 3 P 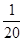

解析试题分析:x的取值是0,1,2,3,其中3天不需要人工降雨的概率是: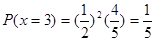 2分
2分
2天不需要人工降雨的概率是: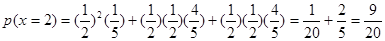 4分
4分
1天不需要人工降雨的概率是: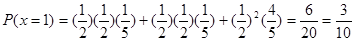 6分
6分
0天不需要人工降雨的概率是: 8分
8分
不需要人工降雨的天数x分布列是
不需要人工降雨的天数x的期望是:x 0 1 2 3 P 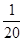

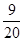
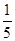
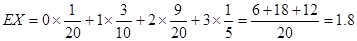 10
10
考点:本题考查了分布列与期望的综合运用
点评:求离散型随机变量的分布列的步骤有:(1)确定离散型随机变量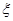 所有的可能取值,并确定
所有的可能取值,并确定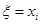 的意义;(2)尽量寻求计算
的意义;(2)尽量寻求计算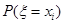 的普遍规律;(3)检查计算结果是否满足分布列的第二条性质
的普遍规律;(3)检查计算结果是否满足分布列的第二条性质

练习册系列答案
相关题目
某市举行一次数学新课程骨干培训活动,共邀请15名使用不同版本教材的数学教师,具体情况数据如下表所示:
| 版本 | 人教A版 | 人教B版 | ||
| 性别 | 男教师 | 女教师 | 男教师 | 女教师 |
| 人数 | 6 |  | 4 | 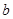 |
现从这15名教师中随机选出2名,则2人恰好是教不同版本的女教师的概率是
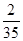 .且
.且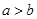 .
.(1)求实数
 ,
,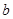 的值
的值(2)培训活动现随机选出2名代表发言,设发言代表中使用人教B版的女教师人数为
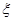 ,求随机变量
,求随机变量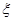 的分布列和数学期望
的分布列和数学期望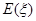 .
. 某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) |  | 30 | 25 |  | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
(Ⅰ)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(Ⅱ)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.(注:将频率视为概率)

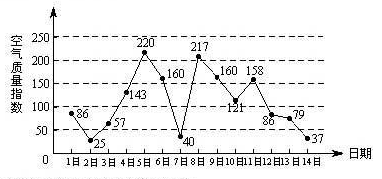
 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组 ,规定
,规定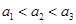
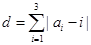 ,(其中
,(其中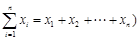 ,从所有三元有序数组中任选一个,求它的“项标距离”
,从所有三元有序数组中任选一个,求它的“项标距离”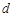 为偶数的概率;
为偶数的概率;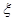 ;乙用这枚硬币掷2次,记正面朝上的次数为
;乙用这枚硬币掷2次,记正面朝上的次数为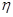 。
。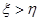 ,则甲获胜;若
,则甲获胜;若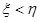 ,则乙获胜,分别求出甲和乙获胜的概率.
,则乙获胜,分别求出甲和乙获胜的概率.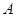 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为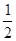 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区