Question

已知偶函数f(x)在区间[0，＋∞)单调递增，则满足f(2x－1)<f的x取值范围是  (　　)

A．          B．          C．          D．

 

Answer 1

【答案】

A

【解析】

试题分析：根据题意，由于偶函数f(x)在区间[0，＋∞)单调递增，那么可知在对称区间x<0上单调递减，同时利用偶函数的对称性可知，要使得f(2x－1)<f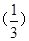，只要||2x-1|<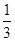,解得x取值范围是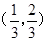故选A

考点：抽象函数的性质

点评：本题给出抽象函数为偶函数且在[0，+∞）上为增函数，求关于x的不等式的解集，着重考查了函数单调性的奇偶性等知识，属于基础题．