Question

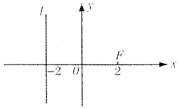
（08年滨州市质检三理） 如图，已知点F（2，0），直线为该平面上的动点，过P做直线l的垂直，垂足为Q，且

   （1）求动点P的轨迹C的方程；

   （2）设过A（－2，0）的直线m交轨迹C于M，N两点，且∠MFN为锐角，求直线m的斜率k的取值范围.

 

Answer 1

解析：   （I）设动点

           

由于

∴动点P的轨迹C的方程为                      

   （II）设消去y并整理得：

    由于直线m与轨迹C交于M，N两点，所以

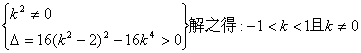      ①

   

    由于，解得

   

    由①②取交集得k的取值范围是