题目内容
设F1、F2,分别是椭圆 的左、右焦点,点P在椭圆上,若|PF1|=9|PF2|,则P点的坐标为 .
的左、右焦点,点P在椭圆上,若|PF1|=9|PF2|,则P点的坐标为 .
【答案】分析:设P(x,y)利用椭圆的第二定义可求得|PF1|,|PF2|,利用|PF1|=9|PF2|即可求得点P的横坐标x,继而可得答案.
解答:解:设P(x,y),
∵椭圆 +
+ =1的右准线l2的方程为x=
=1的右准线l2的方程为x= =
= =
=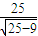 =
= ,
,
∴椭圆 +
+ =1的左准线l1的方程为x=-
=1的左准线l1的方程为x=- ;
;
设点P在l1上的射影为P′,在l2上的射影为P″,
则由椭圆的第二定义得: =
= =e=
=e= =
= ,
,
∴|PF1|= |PP′|=
|PP′|= (x+
(x+ ),
),
同理可得,|PF2|=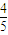 (
( -x),
-x),
∵|PF1|=9|PF2|,
∴ (x+
(x+ )=9×
)=9× (
( -x),
-x),
解得x=5.
∴y=0,
∴P点的坐标为(5,0).
点评:本题考查椭圆的第二定义,考查方程思想与化归思想的综合运用,考查逻辑思维能力与运算能力,属于中档题.
解答:解:设P(x,y),
∵椭圆
 +
+ =1的右准线l2的方程为x=
=1的右准线l2的方程为x= =
= =
=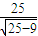 =
= ,
,∴椭圆
 +
+ =1的左准线l1的方程为x=-
=1的左准线l1的方程为x=- ;
;设点P在l1上的射影为P′,在l2上的射影为P″,
则由椭圆的第二定义得:
 =
= =e=
=e= =
= ,
,∴|PF1|=
 |PP′|=
|PP′|= (x+
(x+ ),
),同理可得,|PF2|=
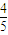 (
( -x),
-x),∵|PF1|=9|PF2|,
∴
 (x+
(x+ )=9×
)=9× (
( -x),
-x),解得x=5.
∴y=0,
∴P点的坐标为(5,0).
点评:本题考查椭圆的第二定义,考查方程思想与化归思想的综合运用,考查逻辑思维能力与运算能力,属于中档题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 的左、右焦点,点P在椭圆上,若|PF1|=9|PF2|,则P点的坐标为________.
的左、右焦点,点P在椭圆上,若|PF1|=9|PF2|,则P点的坐标为________.