题目内容
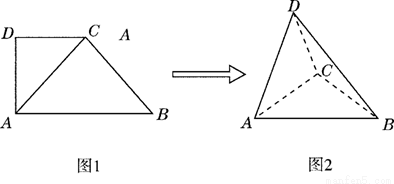
如图 ,在直角梯形
,在直角梯形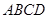 中,
中,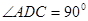 ,
,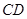 ∥
∥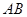 ,
,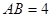 ,
,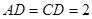 ,将
,将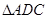 沿
沿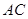 折起,使平面
折起,使平面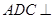 平面
平面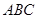 ,得到几何体
,得到几何体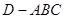 ,如图2所示.
,如图2所示.
(Ⅰ)求证: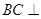 平面
平面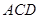 ;
;
(Ⅱ)求几何体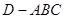 的体积.
的体积.
【答案】
(Ⅰ)详见解析; (Ⅱ) 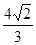 .
.
【解析】
试题分析:(Ⅰ) 先证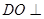 平面
平面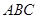 ,再根据
,再根据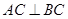 即可证
即可证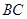 ⊥平面
⊥平面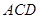 ; (Ⅱ)先分析知
; (Ⅱ)先分析知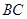 为三棱锥
为三棱锥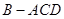 的高,再求得
的高,再求得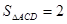 ,即可得
,即可得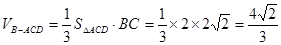 .
.
试题解析:(Ⅰ)证明:在图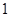 中,可得
中,可得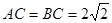 ,从而
,从而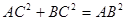 ,故
,故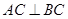 ,取
,取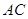 的中点
的中点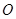 ,连接
,连接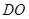 ,则
,则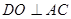 ,又平面
,又平面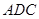 ⊥平面
⊥平面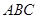 ,平面
,平面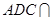 平面
平面 ,
, 平面
平面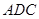 ,从而
,从而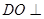 平面
平面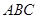 ,∴
,∴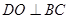 ,又
,又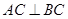 ,
,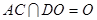 ,∴
,∴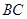 ⊥平面
⊥平面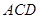 .
.
(Ⅱ)解 由(Ⅰ)知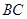 为三棱锥
为三棱锥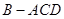 的高,
的高,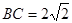 ,
,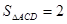 ,
,
∴ 由等体积性可知,几何体
由等体积性可知,几何体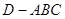 的体积为
的体积为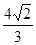 .
.
考点:1.直线与平面垂直;2.体积.

练习册系列答案
相关题目

 中,
中, ∥
∥ ,
,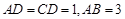 ,动点
,动点 在
在 内运动(含边界),设
内运动(含边界),设 ,则
,则 的最大值是 .
的最大值是 .
 中,
中, ,
, ,
, .将
.将 沿
沿 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
 平面
平面 ;(2) 求几何体
;(2) 求几何体 中,
中, ,
, ,
, ,
,  为线段
为线段 的中点.将
的中点.将 沿
沿 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
 平面
平面 ;
; 的余弦值.
的余弦值.
 中,
中, ,
, ,
, ,
, .将
.将 所在的直线旋转一周,形成一个几何体.
所在的直线旋转一周,形成一个几何体. ;
;
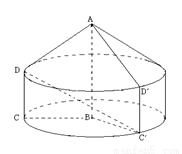 (2)设直角梯形
(2)设直角梯形 (
( )至
)至 ,问:是否存在
,问:是否存在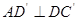 .若存在,求角
.若存在,求角