题目内容
对于每个正整数n,抛物线y=(n2+n)x2-(2n+1)x+1与x轴交于An,Bn两点,以|AnBn|表示An,Bn两点间的距离,则|A1B1|+|A2B2|+…+|A2013B2013|的值是( )A.

B.

C.

D.

【答案】分析:由于y=(n2+n)x2-(2n+1)x+1=(nx-1)[(n+1)x-1],于是|AnBn|=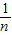 -
-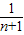 ,利用累加法即可求和即可.
,利用累加法即可求和即可.
解答:解:∵y=(n2+n)x2-(2n+1)x+1=(nx-1)[(n+1)x-1],
∴由y=0得:x=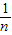 或x=
或x=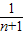 ,
,
∴An(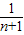 ,0),Bn(
,0),Bn(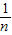 ,0),
,0),
∴|AnBn|=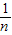 -
-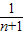 ,
,
∴|A1B1|+|A2B2|+…+|A2013B2013|=(1- )+(
)+( -
- )+(
)+( -
- )+…+(
)+…+(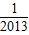 -
-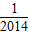 )
)
=1-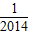 =
=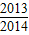 .
.
故选C.
点评:本题考查数列与函数的综合,难点在于明确|AnBn|=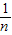 -
-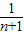 ,考查学生分析问题与转化求解的能力,属于中档题.
,考查学生分析问题与转化求解的能力,属于中档题.
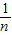 -
-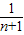 ,利用累加法即可求和即可.
,利用累加法即可求和即可.解答:解:∵y=(n2+n)x2-(2n+1)x+1=(nx-1)[(n+1)x-1],
∴由y=0得:x=
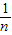 或x=
或x=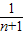 ,
,∴An(
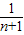 ,0),Bn(
,0),Bn(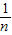 ,0),
,0),∴|AnBn|=
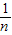 -
-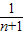 ,
,∴|A1B1|+|A2B2|+…+|A2013B2013|=(1-
 )+(
)+( -
- )+(
)+( -
- )+…+(
)+…+(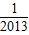 -
-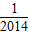 )
)=1-
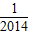 =
=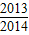 .
.故选C.
点评:本题考查数列与函数的综合,难点在于明确|AnBn|=
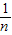 -
-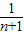 ,考查学生分析问题与转化求解的能力,属于中档题.
,考查学生分析问题与转化求解的能力,属于中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目