题目内容
对于每个正整数n,抛物线y=(n2+n)x2-(2n+1)x+1与x轴交于两点An、Bn,则|A1B1|+|A2B2|+…+|A2010B2010|的值为
【答案】分析:An、Bn,是抛物线y=(n2+n)x2-(2n+1)x+1与x轴的交点,所以其横坐标为(n2+n)x2-(2n+1)x+1=0的根,由根与系数的关系可得,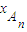 +
+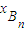 =
=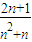 ,
,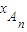
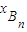 =
=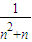 因为|AnBn|=|
因为|AnBn|=|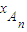 -
-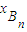 |,将其用两根之和与两根之积表示出来,化简即可得出线段|AnBn|的表达式.
|,将其用两根之和与两根之积表示出来,化简即可得出线段|AnBn|的表达式.
解答:解:由已知An、Bn的横坐标为(n2+n)x2-(2n+1)x+1=0的根,
由根与系数的关系可得,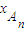 +
+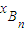 =
=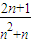 ,
,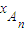
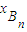 =
=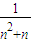 ①
①
因为|AnBn|=|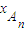 -
-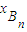 |=
|= ②
②
将①中的数据代入②整理得|AnBn|=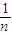 -
-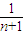
故|A1B1|+|A2B2|+…+|A2010B2010|=1- +
+ -
- +…+
+…+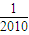 -
-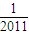 =
=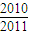
故应填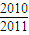 .
.
点评:本题主要考查零点与方程根的对应关系及化简计算的能力,变形的技巧,可以之训练答题者观察探究的能力与意识.
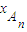 +
+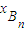 =
=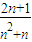 ,
,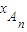
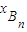 =
=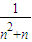 因为|AnBn|=|
因为|AnBn|=|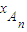 -
-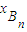 |,将其用两根之和与两根之积表示出来,化简即可得出线段|AnBn|的表达式.
|,将其用两根之和与两根之积表示出来,化简即可得出线段|AnBn|的表达式.解答:解:由已知An、Bn的横坐标为(n2+n)x2-(2n+1)x+1=0的根,
由根与系数的关系可得,
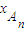 +
+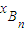 =
=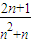 ,
,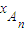
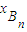 =
=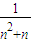 ①
①因为|AnBn|=|
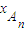 -
-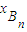 |=
|= ②
②将①中的数据代入②整理得|AnBn|=
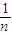 -
-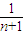
故|A1B1|+|A2B2|+…+|A2010B2010|=1-
 +
+ -
- +…+
+…+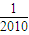 -
-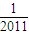 =
=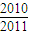
故应填
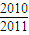 .
.点评:本题主要考查零点与方程根的对应关系及化简计算的能力,变形的技巧,可以之训练答题者观察探究的能力与意识.

练习册系列答案
相关题目



