题目内容
(理)若圆M:(x-a)2+(y-b)2=6与圆N:(x+1)2+(y+1)2=5的两个交点始终为圆N:(x+1)2+(y+1)2=5的直径两个端点,则动点M(a,b)的轨迹方程为 .
分析:圆M:(x-a)2+(y-b)2=6的圆心到圆N:x+1)2+(y+1)2=5的圆心的距离是定值,即可得到动点M(a,b)的轨迹方程.
解答:解:过圆M:(x-a)2+(y-b)2=6的圆心坐标M(a,b),圆N:(x+1)2+(y+1)2=5的圆心(-1,-1),
∴圆心距为:
,
∴(
)2=(
)2+(
)2;
即:(a+1)2+(b+1)2=1.
动点M(a,b)的轨迹方程为:(a+1)2+(b+1)2=1.
故答案为::(a+1)2+(b+1)2=1
∴圆心距为:
| (a+1)2+(b+1)2 |
∴(
| 6 |
| 5 |
| (a+1)2+(b+1)2 |
即:(a+1)2+(b+1)2=1.
动点M(a,b)的轨迹方程为:(a+1)2+(b+1)2=1.
故答案为::(a+1)2+(b+1)2=1
点评:本题考查动点的轨迹方程的求法,圆与圆的位置关系的应用,考查计算能力.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
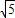 )2+y2=36,定点N(
)2+y2=36,定点N(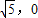 ),点P为圆M上的动点,点G在MP上,且满足|GP|=|GN|
),点P为圆M上的动点,点G在MP上,且满足|GP|=|GN|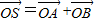 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.