题目内容
(理)已知圆M:(x+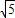 )2+y2=36,定点N(
)2+y2=36,定点N(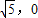 ),点P为圆M上的动点,点G在MP上,且满足|GP|=|GN|
),点P为圆M上的动点,点G在MP上,且满足|GP|=|GN|(1)求点G的轨迹C的方程;
(2)过点(2,0)作直线l,与曲线C交于A、B两点,O是坐标原点,设
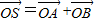 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由.
【答案】分析:(1)由|PG|=|GN|,知|GN|+|GM|=|MP|=6,由椭圆定义可知,点G的轨迹是以M、N为焦点的椭圆,由此能求出点G的轨迹C的方程.
(2)因为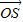 =
=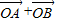 ,所以四边形OASB为平行四边形,假设存在l使得|
,所以四边形OASB为平行四边形,假设存在l使得|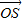 |=|
|=|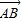 |,则四边形OASB为矩形,故
|,则四边形OASB为矩形,故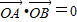 .由此能够推出导出存在直线l的方程为3x-2y-6=0,或3x+2y-6=0,使四边形OASB的对角线相等.
.由此能够推出导出存在直线l的方程为3x-2y-6=0,或3x+2y-6=0,使四边形OASB的对角线相等.
解答:解:(1)∵|PG|=|GN|,∴|GN|+|GM|=|MP|=6,
又∵|MN|=2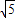 ,∴|GN|+|GM|>|MN|,
,∴|GN|+|GM|>|MN|,
由椭圆定义可知,点G的轨迹是以M、N为焦点的椭圆,
设方程为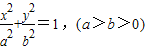 ,
,
则2a=6,2c=2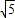 ,∴a=3,c=
,∴a=3,c=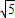 ,b=
,b=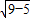 =2,
=2,
∴点G的轨迹方程是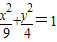 .…(5分)
.…(5分)
(2)因为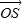 =
=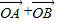 ,所以四边形OASB为平行四边形,
,所以四边形OASB为平行四边形,
假设存在l使得|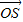 |=|
|=|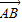 |,则四边形OASB为矩形,
|,则四边形OASB为矩形,
∴ .
.
①当直线l的斜率不存在时,直线l的方程为x=2,
由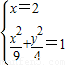 ,得
,得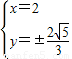 ,
,
此时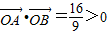 ,或
,或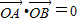 矛盾,不合题意,舍去.
矛盾,不合题意,舍去.
②当直线l的斜率存在时,设l的方程为y=k(x-2),
设A(x1,y1),B(x2,y2),
由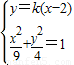 ,得(9k2+4)x2-36k2x+36(k2-1)=0,
,得(9k2+4)x2-36k2x+36(k2-1)=0,
△=(-36k2)2-144(9k2+4)(k2-1)=720k2+576>0.(※)
∴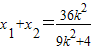 ,
,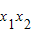 =
=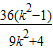 ,①
,①
y1y2=[k(x1-2)][k(x2-2)]
=k2[x1x2-2(x1+x2)+4]
=-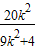 ,②
,②
把①②代入x1x2+y1y2=0,
解得k=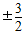 ,代入(※)式,验证成立.
,代入(※)式,验证成立.
∴直线l的方程为y=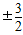 (x-2),即3x-2y-6=0,或3x+2y-6=0,
(x-2),即3x-2y-6=0,或3x+2y-6=0,
故存在直线l的方程为3x-2y-6=0,或3x+2y-6=0,使四边形OASB的对角线相等.
点评:本题考查点的轨迹方程的求法,考查直线方程的求法.解题时要认真审题,仔细解答,注意等价转化思想、分类讨论思想的合理运用.
(2)因为
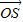 =
=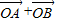 ,所以四边形OASB为平行四边形,假设存在l使得|
,所以四边形OASB为平行四边形,假设存在l使得|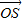 |=|
|=|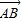 |,则四边形OASB为矩形,故
|,则四边形OASB为矩形,故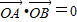 .由此能够推出导出存在直线l的方程为3x-2y-6=0,或3x+2y-6=0,使四边形OASB的对角线相等.
.由此能够推出导出存在直线l的方程为3x-2y-6=0,或3x+2y-6=0,使四边形OASB的对角线相等.解答:解:(1)∵|PG|=|GN|,∴|GN|+|GM|=|MP|=6,
又∵|MN|=2
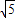 ,∴|GN|+|GM|>|MN|,
,∴|GN|+|GM|>|MN|,由椭圆定义可知,点G的轨迹是以M、N为焦点的椭圆,
设方程为
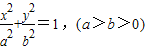 ,
,则2a=6,2c=2
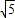 ,∴a=3,c=
,∴a=3,c=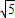 ,b=
,b=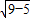 =2,
=2,∴点G的轨迹方程是
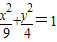 .…(5分)
.…(5分)(2)因为
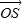 =
=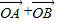 ,所以四边形OASB为平行四边形,
,所以四边形OASB为平行四边形,假设存在l使得|
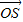 |=|
|=|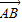 |,则四边形OASB为矩形,
|,则四边形OASB为矩形,∴
 .
.①当直线l的斜率不存在时,直线l的方程为x=2,
由
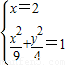 ,得
,得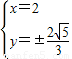 ,
,此时
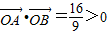 ,或
,或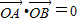 矛盾,不合题意,舍去.
矛盾,不合题意,舍去.②当直线l的斜率存在时,设l的方程为y=k(x-2),
设A(x1,y1),B(x2,y2),
由
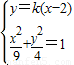 ,得(9k2+4)x2-36k2x+36(k2-1)=0,
,得(9k2+4)x2-36k2x+36(k2-1)=0,△=(-36k2)2-144(9k2+4)(k2-1)=720k2+576>0.(※)
∴
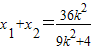 ,
,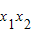 =
=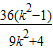 ,①
,①y1y2=[k(x1-2)][k(x2-2)]
=k2[x1x2-2(x1+x2)+4]
=-
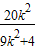 ,②
,②把①②代入x1x2+y1y2=0,
解得k=
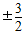 ,代入(※)式,验证成立.
,代入(※)式,验证成立.∴直线l的方程为y=
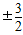 (x-2),即3x-2y-6=0,或3x+2y-6=0,
(x-2),即3x-2y-6=0,或3x+2y-6=0,故存在直线l的方程为3x-2y-6=0,或3x+2y-6=0,使四边形OASB的对角线相等.
点评:本题考查点的轨迹方程的求法,考查直线方程的求法.解题时要认真审题,仔细解答,注意等价转化思想、分类讨论思想的合理运用.

练习册系列答案
相关题目
 (理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足
(理)如图所示,已知圆C:(x+1)2+y2=8,定点A(1,0),M为圆上一动点,点P在AM上,点N在CM上,且满足