题目内容
已知总体服从正态分布N(120,3.62),求满足下列条件的个体在总体中所占的比例.(1)数值不大于129;
(2)数值大于111;
(3)数值在112.8与123.6之间.
解:由正态分布N(120,3.62)得总体平均数μ=120,σ=3.6.
(1)F(129)=Φ(![]() )=Φ(2.5)≈0.9938,即数值不大于129的个体在总体中所占的比例为0.9938.
)=Φ(2.5)≈0.9938,即数值不大于129的个体在总体中所占的比例为0.9938.
(2)F(111)=Φ(![]() )=Φ(-2.5)=1-Φ(2.5),∴1-F(111)=Φ(2.5)≈0.9938.
)=Φ(-2.5)=1-Φ(2.5),∴1-F(111)=Φ(2.5)≈0.9938.
(3)F(123.6)=Φ(![]() )=Φ(1),
)=Φ(1),
F(112.8)=Φ(![]() )=Φ(-2)=1-Φ(2),
)=Φ(-2)=1-Φ(2),
∴F(123.6)-F(112.8)=Φ(1)+Φ(2)-1
≈0.8413+0.9772-1=0.8185,
即数值在112.8与123.6之间的个体在总体中所占的比例为0.8185.
点评:(1)首先利用F(x)=Φ(![]() )转化为标准正态分布,然后注意在计算中灵活运用公式.(2)通过(1)、(2)看出F(129)等于P(x>111),这是由于111与129这两个数关于正态曲线的对称轴x=120对称造成的.
)转化为标准正态分布,然后注意在计算中灵活运用公式.(2)通过(1)、(2)看出F(129)等于P(x>111),这是由于111与129这两个数关于正态曲线的对称轴x=120对称造成的.

练习册系列答案
相关题目
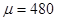 ,标准差
,标准差 ,总体服从正态分布,若云龙一中录取率为40%,那么云龙一中录取分数线可能划在(已知
,总体服从正态分布,若云龙一中录取率为40%,那么云龙一中录取分数线可能划在(已知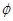 (0.25)=0.6) ( )
(0.25)=0.6) ( ) ,标准差
,标准差 ,总体服从正态分布,若衡水中学录取率为40%,那么衡水中学录取分数线可能划在(已知
,总体服从正态分布,若衡水中学录取率为40%,那么衡水中学录取分数线可能划在(已知 (0.25)=0.6)( )
(0.25)=0.6)( )