题目内容
已知向量 =(a,b),向量
=(a,b),向量 ⊥
⊥ ,且
,且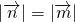 ,则
,则 的坐标可以为 ________(写出一个即可).
的坐标可以为 ________(写出一个即可).
(-b,a)或(b,-a)
分析:设出 的坐标,利用向量垂直的充要条件列出方程,再利用向量模的坐标公式列出方程,解方程组求出.
的坐标,利用向量垂直的充要条件列出方程,再利用向量模的坐标公式列出方程,解方程组求出.
解答:设 ,据题意得
,据题意得
 即ax+by=0①
即ax+by=0①
∵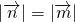 ∴a2+b2=x2+y2②
∴a2+b2=x2+y2②
解得x=b或-b;y=a或-a
故答案为(-b,a)或(b,-a)
点评:本题考查向量垂直的坐标形式的充要条件、向量模的计算公式.
分析:设出
 的坐标,利用向量垂直的充要条件列出方程,再利用向量模的坐标公式列出方程,解方程组求出.
的坐标,利用向量垂直的充要条件列出方程,再利用向量模的坐标公式列出方程,解方程组求出.解答:设
 ,据题意得
,据题意得 即ax+by=0①
即ax+by=0①∵
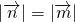 ∴a2+b2=x2+y2②
∴a2+b2=x2+y2②解得x=b或-b;y=a或-a
故答案为(-b,a)或(b,-a)
点评:本题考查向量垂直的坐标形式的充要条件、向量模的计算公式.

练习册系列答案
相关题目
已知向量
=(a,b),向量
⊥
且|
|=|
|,则
的坐标为( )
| m |
| m |
| n |
| m |
| n |
| n |
| A、(a,-b) |
| B、(-a,b) |
| C、(b,-a) |
| D、(-b,-a) |
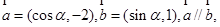 则
则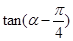 等于(
)
等于(
)  B.
B. C.
C. 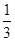 D.
D. 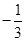
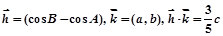 ,其中a、b、c分别是
,其中a、b、c分别是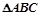 的三内角A、B、C的对边长.
的三内角A、B、C的对边长.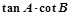 的值;
的值;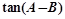 的最大值.
的最大值.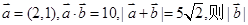 = ( )
= ( )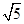 B.
B.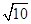 C.5
D.25
C.5
D.25