题目内容
已知命题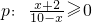
，命题q：x2-2x+1-m2≤0（m＜0），且p是q的必要条件，求实数m的范围．
解：由命题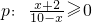，所以，不等式化为
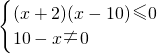，解得p：-2≤x＜10．
命题q：x2-2x+1-m2≤0（m＜0），解得1+m≤x≤1-m；
因为p是q的必要条件，即任意x∈q?x∈p成立，
所以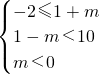
，解得-3≤m＜0；
实数m的范围是：-3≤m＜0．
分析：解分式不等式求出命题p，二次不等式求出q，利用p是q的必要条件得到不等式组，求出m的范围即可．
点评：本题考查充分条件、必要条件和充要条件，解题时要认真审题，仔细解答，注意不等式组的合理运用．
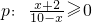，所以，不等式化为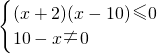，解得p：-2≤x＜10．命题q：x2-2x+1-m2≤0（m＜0），解得1+m≤x≤1-m；
因为p是q的必要条件，即任意x∈q?x∈p成立，
所以
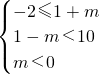，解得-3≤m＜0；实数m的范围是：-3≤m＜0．
分析：解分式不等式求出命题p，二次不等式求出q，利用p是q的必要条件得到不等式组，求出m的范围即可．
点评：本题考查充分条件、必要条件和充要条件，解题时要认真审题，仔细解答，注意不等式组的合理运用．
练习册系列答案
相关题目
，命题q：(x＋a)(x－3)＞0，若p是q的充分不必要条件，则实数a的取值范围是
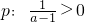；命题q：?x∈R，x2+2ax+2-a=0．若命题“￢p且q”是真命题，求实数a的取值范围．