题目内容
设f(x)=x4-8x3+24x2-32x+16,g(x)=sin( x),则方程f(x)-g(x)=0的所有根之和为
x),则方程f(x)-g(x)=0的所有根之和为
- A.8
- B.6
- C.4
- D.2
C
分析:由f(x)=x4-8x3+24x2-32x+16=(x-2)2,知函数f(x)的对称轴为x=2,由g(x)=sin( x),知函数g(x)的周期为8,一条对称轴为x=2,由此利用数形结合思想能求出方程f(x)-g(x)=0的所有根之和.
x),知函数g(x)的周期为8,一条对称轴为x=2,由此利用数形结合思想能求出方程f(x)-g(x)=0的所有根之和.
解答: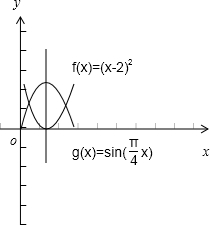 解:∵f(x)=x4-8x3+24x2-32x+16=(x-2)2,
解:∵f(x)=x4-8x3+24x2-32x+16=(x-2)2,
∴函数f(x)的对称轴为x=2,
∵g(x)=sin( x),
x),
∴函数g(x)的周期为8,一条对称轴为x=2,
在同一平面直角坐标系中,分别作出f(x)=(x-2)2和g(x)=sin( x)的图象,
x)的图象,
观察这两个函数的图象,知方程f(x)-g(x)=0有两个根x1和x2,
且x1和x2关于直线x=2对称,
∴x1+x2=4.
故选C.
点评:本题考查函数的所有根之和的求法,解题时要认真审题,仔细解答,注意数形结合思想的合理运用.
分析:由f(x)=x4-8x3+24x2-32x+16=(x-2)2,知函数f(x)的对称轴为x=2,由g(x)=sin(
 x),知函数g(x)的周期为8,一条对称轴为x=2,由此利用数形结合思想能求出方程f(x)-g(x)=0的所有根之和.
x),知函数g(x)的周期为8,一条对称轴为x=2,由此利用数形结合思想能求出方程f(x)-g(x)=0的所有根之和.解答:
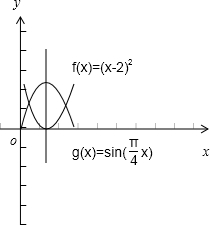 解:∵f(x)=x4-8x3+24x2-32x+16=(x-2)2,
解:∵f(x)=x4-8x3+24x2-32x+16=(x-2)2,∴函数f(x)的对称轴为x=2,
∵g(x)=sin(
 x),
x),∴函数g(x)的周期为8,一条对称轴为x=2,
在同一平面直角坐标系中,分别作出f(x)=(x-2)2和g(x)=sin(
 x)的图象,
x)的图象,观察这两个函数的图象,知方程f(x)-g(x)=0有两个根x1和x2,
且x1和x2关于直线x=2对称,
∴x1+x2=4.
故选C.
点评:本题考查函数的所有根之和的求法,解题时要认真审题,仔细解答,注意数形结合思想的合理运用.

练习册系列答案
相关题目