题目内容
已知函数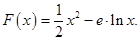
(I)求函数 的极值;
的极值;
(II)对于函数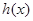 和
和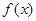 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数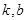 ,使得不等式
,使得不等式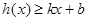 和
和 都成立,则称直线
都成立,则称直线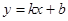 是函数
是函数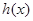 和
和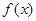 的“分界线”.
的“分界线”.
设函数 ,
,
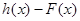 ,试问函数
,试问函数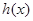 和
和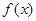 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
【答案】
(I)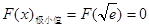 ,
, 无极大值;(II)函数
无极大值;(II)函数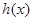 和
和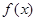 存在“分界线”,方程为
存在“分界线”,方程为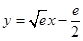 .
.
【解析】
试题分析:(I)首先求函数 的定义域,解方程
的定义域,解方程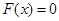 得
得 可能的极值点,进一步得
可能的极值点,进一步得 的单调性,最后根据导函数在零点附近的变号情况求
的单调性,最后根据导函数在零点附近的变号情况求 的极值;(II)函数
的极值;(II)函数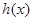 和
和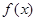 的图象在
的图象在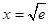 处有公共点
处有公共点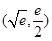 .设函数
.设函数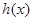 和
和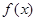 存在“分界线”,方程为
存在“分界线”,方程为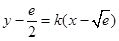 ,由
,由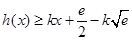 对任意
对任意 恒成立,确定常数
恒成立,确定常数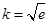 ,从而得“分界线”的方程为
,从而得“分界线”的方程为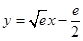 ,再证明
,再证明 在
在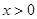 时也恒成立,最后确定函数
时也恒成立,最后确定函数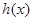 和
和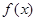 的“分界线”就是直线
的“分界线”就是直线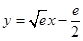 .
.
试题解析:(I)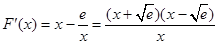 .
. 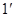
令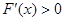 得
得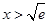 ,
,
所以 在
在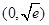 上单调递减,
上单调递减,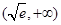 上单调递增,
上单调递增, 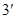
又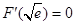 ,
, 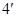
所以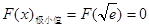 ,
, 无极大值.
无极大值. 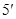
(II)由(I)知 ,
,
所以函数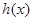 和
和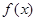 的图象在
的图象在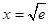 处有公共点
处有公共点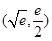 .
. 
设函数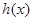 和
和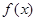 存在“分界线”,方程为
存在“分界线”,方程为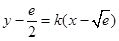 ,
,
应有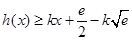 对任意
对任意 恒成立,即
恒成立,即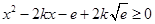 在
在 时恒成立,
时恒成立,
于是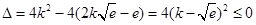 ,得
,得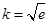 ,
,
则“分界线”的方程为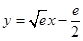 .
. 
记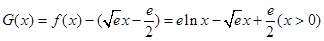 ,则
,则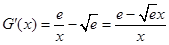
令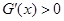 得
得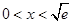 ,所以
,所以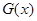 在
在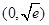 上单调递增,
上单调递增,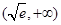 上单调递减,
上单调递减,
当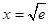 时,函数
时,函数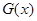 取得最大值
取得最大值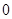 ,即
,即 在
在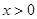 时恒成立.
时恒成立. 
综上所述,函数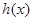 和
和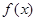 存在“分界线”,方程为
存在“分界线”,方程为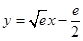 ……
……
考点:1、应用导数求函数极值(最值);2、应用导数研究函数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的 部 分 图 象如 图 所示.
的 部 分 图 象如 图 所示. 的
解 析 式;
的
解 析 式; 中,角
中,角 的
对 边 分 别 是
的
对 边 分 别 是 ,若
,若 的
取 值 范 围.
的
取 值 范 围.