题目内容
已知a>0,b>0,且a≠b,比较 +
+ 与a+b的大小.
与a+b的大小.
解:∵( +
+ )-(a+b)=
)-(a+b)= -b+
-b+ -a
-a
= +
+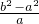
=(a2-b2)( -
- )
)
=(a2-b2)
=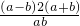 ,
,
又∵a>0,b>0,a≠b,∴(a-b)2>0,a+b>0,ab>0.
∴( +
+ )-(a+b)>0,
)-(a+b)>0,
∴ +
+ >a+b.
>a+b.
分析:通过作差化简判断符号,即可比较出此两个数的大小.
点评:作差法是比较两个数大小最常用的方法,必须掌握.正确化简是关键.
 +
+ )-(a+b)=
)-(a+b)= -b+
-b+ -a
-a=
 +
+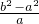
=(a2-b2)(
 -
- )
)=(a2-b2)

=
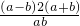 ,
,又∵a>0,b>0,a≠b,∴(a-b)2>0,a+b>0,ab>0.
∴(
 +
+ )-(a+b)>0,
)-(a+b)>0,∴
 +
+ >a+b.
>a+b.分析:通过作差化简判断符号,即可比较出此两个数的大小.
点评:作差法是比较两个数大小最常用的方法,必须掌握.正确化简是关键.

练习册系列答案
相关题目