Question

4．已知四面体ABCD中，AB=AC，BD=CD，平面ABC⊥平面BCD，E，F分别为棱BC和AD的中点．
（1）求证：AE⊥平面BCD；
（2）求证：AD⊥BC；
（3）若△ABC内的点G满足FG∥平面BCD，设点G构成集合T，试描述点集 的位置（不必说明理由）．

Answer 1

分析 （1）由题意可证AE⊥BC，由面面垂直的性质即可证明AE⊥平面BCD．
（2）先证明BC⊥DE，由（1）知AE⊥BC，由判定定理可得BC⊥平面AED，由线面垂直的性质即可证明BD⊥AD．
（3）由线面平行的判定定理可得取AB、AC的中点M、N，所有的点G构成的集合T即为△ABC的中位线MN．

解答 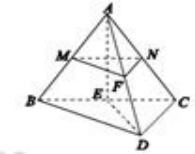证明：（1）∵在△ABC中，AB=AC，E为BC的中点，
∴AE⊥BC．
又∵平面ABC⊥平面BCD，AE?平面ABC，平面ABC∩平面BCD=BC，
∴AE⊥平面BCD．
（2）∵BD=CD，E为BC的中点，
∴BC⊥DE．
由（1）知AE⊥BC，又AE∩DE=E，AE，DE?平面AED，
∴BC⊥平面AED，又AD?平面AED，
∴BD⊥AD．
（3）取AB、AC的中点M、N，所有的点G构成的集合T即为△ABC的中位线MN．

点评 本题主要考查了直线与平面平行的判定，直线与平面垂直的判定，考查了空间想象能力和转化思想，属于基本知识的考查．