Question

【题目】已知函数，

(1)写出它的振幅、周期、初相；

(2)用“五点法”作出它在一个周期内的图象；

(3)说明的图象可由的图象经过怎样的变换而得到。

Answer 1

【答案】(1)A＝2，T＝π，φ＝；(2)见解析；(3) )见解析；

【解析】

（1）根据振幅，周期，初相的定义得到对应的值；（2）设X＝2x＋，由X取0，，π，，2π来求出相应的x，通过列表，计算得出五点坐标，描点后得出图象；（3）根据左加右减的原则，以及伸缩变换得到图像的变换.

(1)y＝2sin的振幅A＝2，

周期T＝＝π，初相φ＝.

(2)令X＝2x＋，则y＝2sin＝2sinX.

列表如下：

x	－
X	0		π		2π
y＝sinX	0	1	0	－1	0
y＝2sin	0	2	0	－2	0

描点画出图象，如图所示：

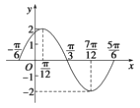
(3)把y＝sinx的图象上所有的点向左平移个单位长度，得到y＝sin的图象；

再把y＝sin的图象上所有点的横坐标缩短到原来的倍(纵坐标不变)，得到y＝sin的图象；最后把y＝sin上所有点的纵坐标伸长到原来的2倍(横坐标不变)，即可得到y＝2sin的图象．