��Ŀ����
ij�л����о�����������ÿ�컷����Ⱦ������е����о�����һ���л����ۺ���Ⱦָ��f��x����ʱ��x��Сʱ���Ĺ�ϵΪf(x)=|
sin(
x)+
-a|+2a��x��[0��24]������aΪ�������йصIJ�������a��[0��
]������ÿ��f��x�������ֵ��Ϊ������ۺ���Ⱦָ����������M��a����
������t=
sin(
x)��x��[0��24]����t��ȡֵ��Χ��
��������M��a����
����Ϊ��ǿ�Ի�����Ⱦ�����Σ��������涨ÿ����ۺϻ�����Ⱦָ�����ó���2������Ŀǰ�����ĵ��ۺ���Ⱦָ���Ƕ��٣��Ƿꣿ
| 1 |
| 2 |
| �� |
| 32 |
| 1 |
| 3 |
| 3 |
| 4 |
������t=
| 1 |
| 2 |
| �� |
| 32 |
��������M��a����
����Ϊ��ǿ�Ի�����Ⱦ�����Σ��������涨ÿ����ۺϻ�����Ⱦָ�����ó���2������Ŀǰ�����ĵ��ۺ���Ⱦָ���Ƕ��٣��Ƿꣿ
��������I������x��ȡֵ��Χ���
��ȡֵ��Χ�����������Һ��������ʴӶ������t��ȡֵ��Χ��
�����ɣ�I������f��x���Ľ���ʽ������a�ķ�Χ��ȥ������ֵ���Ӷ��������M��a����
�����ݷֶκ������ֱ��о�ÿ���ϵ����ֵ��Ȼ����2���бȽϣ��Ӷ�ȷ���Ƿ꣮
| ��x |
| 32 |
�����ɣ�I������f��x���Ľ���ʽ������a�ķ�Χ��ȥ������ֵ���Ӷ��������M��a����
�����ݷֶκ������ֱ��о�ÿ���ϵ����ֵ��Ȼ����2���бȽϣ��Ӷ�ȷ���Ƿ꣮
����⣺����x��[0��24]��
��[0��
]��t��[0��
]�� ������4�֣�
������g(t)=|t+
-a|+2a=|t-(a-
)|+2a��t��[0��
]��
��a-
��
��0��a��
ʱ��(g(t))max=g(
)=|
-a|+2a=a+
�� ����6�֣�
��a-
��
��
��a��
ʱ��(g(t))max=g(0)=|
-a|+2a=3a-
�� ����8�֣�
M��a��=
����10�֣�
����a��[0��
)ʱ��M��a������������M(a)��M(
)=
��2����11�֣�
��a��[
��
]ʱ��M��a������������M(a)��M(
)=
��2������13�֣�
���ԣ���������Ⱦָ��û�г��� ����15�֣�
| ��x |
| 32 |
| 3�� |
| 4 |
| 1 |
| 2 |
������g(t)=|t+
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
��a-
| 1 |
| 3 |
| 1 |
| 4 |
| 7 |
| 12 |
| 1 |
| 2 |
| 5 |
| 6 |
| 5 |
| 6 |
��a-
| 1 |
| 3 |
| 1 |
| 4 |
| 7 |
| 12 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
M��a��=
|
����a��[0��
| 7 |
| 12 |
| 7 |
| 12 |
| 17 |
| 12 |
��a��[
| 7 |
| 12 |
| 3 |
| 4 |
| 3 |
| 4 |
| 23 |
| 12 |
���ԣ���������Ⱦָ��û�г��� ����15�֣�
������������Ҫ�����˸���ʵ������ѡ�������ͣ��Լ����õ���������ֵ��ͬʱ�����˼��������ͷ������۵���ѧ˼�룬�����е��⣮

��ϰ��ϵ�д�
�����Ŀ
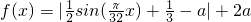 ��x��[0��24]������aΪ�������йصIJ�������a��[0��
��x��[0��24]������aΪ�������йصIJ�������a��[0�� ]������ÿ��f��x�������ֵ��Ϊ������ۺ���Ⱦָ����������M��a����
]������ÿ��f��x�������ֵ��Ϊ������ۺ���Ⱦָ����������M��a���� ��x��[0��24]����t��ȡֵ��Χ��
��x��[0��24]����t��ȡֵ��Χ��