题目内容
某市环境研究所对市中心每天环境污染情况进行调查研究后,发现一天中环境综合污染指数f(x)与时间x(小时)的关系为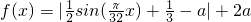 ,x∈[0,24],其中a为与气象有关的参数,且a∈[0,
,x∈[0,24],其中a为与气象有关的参数,且a∈[0, ].若用每天f(x)的最大值作为当天的综合污染指数,并记作M(a).
].若用每天f(x)的最大值作为当天的综合污染指数,并记作M(a).
(Ⅰ)令 ,x∈[0,24],求t的取值范围;
,x∈[0,24],求t的取值范围;
(Ⅱ)求函数M(a);
(Ⅲ)为加强对环境污染的整治,市政府规定每天的综合环境污染指数不得超过2,试问目前市中心的综合污染指数是多少?是否超标?
解:(Ⅰ)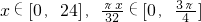 ,
, . …
. …
(Ⅱ)令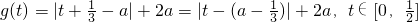 .
.
当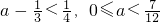 时,
时,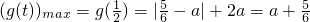 . …
. …
当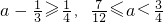 时,
时, . …
. …
M(a)=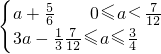 …
…
(Ⅲ)当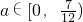 时,M(a)是增函数,
时,M(a)是增函数,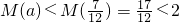 …
…
当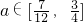 时,M(a)是增函数,
时,M(a)是增函数,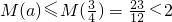 .…
.…
所以,市中心污染指数没有超标 …
分析:(I)根据x的取值范围求出 的取值范围,最后根据正弦函数的性质从而可求出t的取值范围;
的取值范围,最后根据正弦函数的性质从而可求出t的取值范围;
(Ⅱ)由(I)化简f(x)的解析式,讨论a的范围,去掉绝对值,从而求出函数M(a);
(Ⅲ)根据分段函数,分别研究每段上的最大值,然后与2进行比较,从而确定是否超标.
点评:本题主要考查了根据实际问题选择函数类型,以及利用单调性求最值,同时考查了计算能力和分类讨论的数学思想,属于中档题.
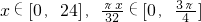 ,
, . …
. …(Ⅱ)令
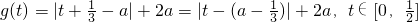 .
.当
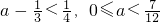 时,
时,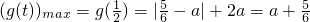 . …
. …当
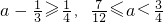 时,
时, . …
. …M(a)=
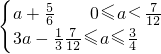 …
…(Ⅲ)当
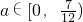 时,M(a)是增函数,
时,M(a)是增函数,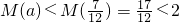 …
…当
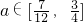 时,M(a)是增函数,
时,M(a)是增函数,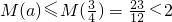 .…
.…所以,市中心污染指数没有超标 …
分析:(I)根据x的取值范围求出
 的取值范围,最后根据正弦函数的性质从而可求出t的取值范围;
的取值范围,最后根据正弦函数的性质从而可求出t的取值范围;(Ⅱ)由(I)化简f(x)的解析式,讨论a的范围,去掉绝对值,从而求出函数M(a);
(Ⅲ)根据分段函数,分别研究每段上的最大值,然后与2进行比较,从而确定是否超标.
点评:本题主要考查了根据实际问题选择函数类型,以及利用单调性求最值,同时考查了计算能力和分类讨论的数学思想,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
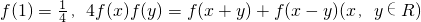 ,则f(2012)=
,则f(2012)=



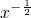 =________.
=________.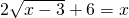 .
. }
}