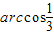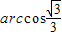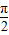题目内容
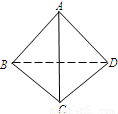
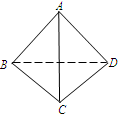 如图,四面体A-BCD的四个面全等,且AB=AC=2
如图,四面体A-BCD的四个面全等,且AB=AC=2| 3 |
分析:取BC的中点为O,连接OA,OD,根据几何体的结构特征可得:BD=CD=2
,AD=4,即可得到OA⊥BC,OD⊥BC,所以∠AOD为所求角,把其放入△AOD中,进而利用解三角形的有关知识求出二面角的平面角得到答案.
| 3 |
解答:解:取BC的中点为O,连接OA,OD,
因为四面体A-BCD的四个面全等,且AB=AC=2
,BC=4,
所以BD=CD=2
,AD=4,
所以OA⊥BC,OD⊥BC,
所以∠AOD为所求角.
因为AB=AC=BD=CD=2
,BC=4,
所以OA=OD=2
,
在△AOD中,AD=4,
所以cos∠AOD=
=0,
所以∠AOD=
.
故选C.
因为四面体A-BCD的四个面全等,且AB=AC=2
| 3 |
所以BD=CD=2
| 3 |
所以OA⊥BC,OD⊥BC,
所以∠AOD为所求角.
因为AB=AC=BD=CD=2
| 3 |
所以OA=OD=2
| 2 |
在△AOD中,AD=4,
所以cos∠AOD=
| OA2+OD2-AD2 |
| 2AO•OD |
所以∠AOD=
| π |
| 2 |
故选C.
点评:本题主要考查二面角的平面角,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键,有时根据几何体的结构特征也可以建立空间直角坐标系利用向量的有关知识解决空间角等问题.

练习册系列答案
相关题目
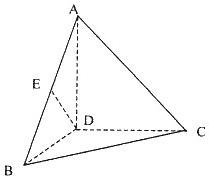 如图,四面体A-BCD中,AD⊥BD,AD⊥CD,BD⊥CD,且AD=BD=CD=2,点E是线段AB的中点.
如图,四面体A-BCD中,AD⊥BD,AD⊥CD,BD⊥CD,且AD=BD=CD=2,点E是线段AB的中点. 如图,四面体A-BCD的四个面全等,且AB=AC=
如图,四面体A-BCD的四个面全等,且AB=AC= ,BC=4,则以BC为棱,以面BCD与面BCA为面的二面角的大小为
,BC=4,则以BC为棱,以面BCD与面BCA为面的二面角的大小为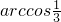
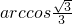


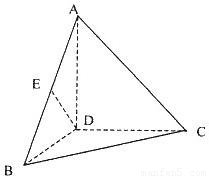
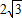 ,BC=4,则以BC为棱,以面BCD与面BCA为面的二面角的大小为( )
,BC=4,则以BC为棱,以面BCD与面BCA为面的二面角的大小为( )