题目内容
已知椭圆 ,过椭圆
,过椭圆 上一点
上一点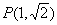 作倾斜角互补的两条直线
作倾斜角互补的两条直线 、
、 ,分别交椭圆
,分别交椭圆 于
于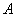 、
、 两点.则直线
两点.则直线 的斜率为 .
的斜率为 .
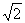
解析试题分析:这题有一定的难度,考查的直线与圆锥曲线相交问题,考查同学们的计算打理能力,当然在解题时注意过程的简捷性,设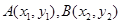 ,同时设
,同时设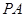 的方程为
的方程为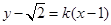 ,代入椭圆方程化简得:
,代入椭圆方程化简得: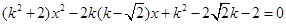 ,显然
,显然 和
和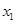 是这个方程的两解,因此
是这个方程的两解,因此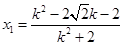 ,
, ,用
,用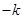 代替
代替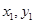 中的
中的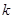 ,得
,得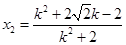 ,
,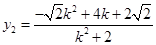 .所以
.所以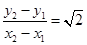 .
.
考点:直线与圆锥曲线相交,直线的斜率.

练习册系列答案
相关题目
 轴上,一个顶点为
轴上,一个顶点为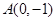 ,其右焦点到直线
,其右焦点到直线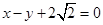 的距离为
的距离为 ,则椭圆的方程为 .
,则椭圆的方程为 . =1的右焦点,且平行于经过一、三象限的渐近线的直线方程是________.
=1的右焦点,且平行于经过一、三象限的渐近线的直线方程是________. 分别是双曲线
分别是双曲线 的左右焦点,
的左右焦点,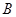 是虚轴的端点,直线
是虚轴的端点,直线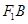 与双曲线
与双曲线 的两条渐近线分别交于
的两条渐近线分别交于 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与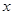 轴交于点
轴交于点 ,若
,若 ,则双曲线
,则双曲线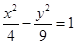 的渐近线方程是 .
的渐近线方程是 . ,
, 是椭圆
是椭圆 的左、右焦点,过
的左、右焦点,过 ,
, 两点,若
两点,若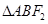 的周长为
的周长为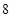 ,则
,则 的值为 .
的值为 .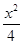 +y2=1的左焦点,O为坐标原点,点P在椭圆上,则
+y2=1的左焦点,O为坐标原点,点P在椭圆上,则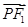 ·
·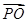 的最大值为________.
的最大值为________.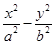 =1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________.
=1(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A,B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是________. ,(φ为参数,a>b>0),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为ρsin (θ+
,(φ为参数,a>b>0),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l与圆O的极坐标方程分别为ρsin (θ+ )=
)= m(m为非零数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为________.
m(m为非零数)与ρ=b.若直线l经过椭圆C的焦点,且与圆O相切,则椭圆C的离心率为________.