题目内容
已知点(2,3)与抛物线 的焦点的距离是5,那么P= .
的焦点的距离是5,那么P= .
12
解析试题分析:抛物线 的焦点为
的焦点为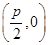 ,点(2,3)到焦点
,点(2,3)到焦点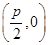 的距离为
的距离为 ,解得
,解得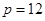 或
或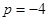 (舍去).
(舍去).
考点:抛物线的定义、两点间的距离公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知点(2,3)与抛物线 的焦点的距离是5,那么P= .
的焦点的距离是5,那么P= .
12
解析试题分析:抛物线 的焦点为
的焦点为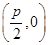 ,点(2,3)到焦点
,点(2,3)到焦点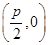 的距离为
的距离为 ,解得
,解得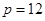 或
或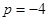 (舍去).
(舍去).
考点:抛物线的定义、两点间的距离公式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案