题目内容
玻璃球盒中装有各色球12只,其中5红、4黑、2白、1绿,从中取1球,求:(1)红或黑的概率;(2)红或黑或白的概率.
(1)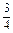 (2)
(2)
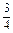 (2)
(2)
方法一 记事件A1:从12只球中任取1球得红球;
A2:从12只球中任取1球得黑球;
A3:从12只球中任取1球得白球;
A4:从12只球中任取1球得绿球,则
P(A1)= ,P(A2)=
,P(A2)=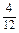 ,P(A3)=
,P(A3)= ,P(A4)=
,P(A4)=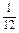 .
.
根据题意,A1、A2、A3、A4彼此互斥,
由互斥事件概率加法公式得
(1)取出红球或黑球的概率为
P(A1+A2)=P(A1)+P(A2)= +
+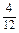 =
=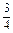 .
.
(2)取出红或黑或白球的概率为
P(A1+A2+A3)=P(A1)+P(A2)+P(A3)
= +
+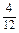 +
+ =
=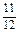 .
.
方法二 (1)取出红球或黑球的对立事件为取出白球或绿球,即A1+A2的对立事件为A3+A4,
∴取出红球或黑球的概率为
P(A1+A2)=1-P(A3+A4)=1-P(A3)-P(A4)
=1- -
-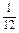 =
= =
=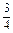 .
.
(2)A1+A2+A3的对立事件为A4.
P(A1+A2+A3)=1-P(A4)=1-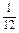 =
=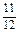 .
.
A2:从12只球中任取1球得黑球;
A3:从12只球中任取1球得白球;
A4:从12只球中任取1球得绿球,则
P(A1)=
 ,P(A2)=
,P(A2)=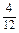 ,P(A3)=
,P(A3)= ,P(A4)=
,P(A4)=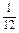 .
.根据题意,A1、A2、A3、A4彼此互斥,
由互斥事件概率加法公式得
(1)取出红球或黑球的概率为
P(A1+A2)=P(A1)+P(A2)=
 +
+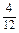 =
=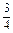 .
.(2)取出红或黑或白球的概率为
P(A1+A2+A3)=P(A1)+P(A2)+P(A3)
=
 +
+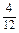 +
+ =
=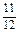 .
.方法二 (1)取出红球或黑球的对立事件为取出白球或绿球,即A1+A2的对立事件为A3+A4,
∴取出红球或黑球的概率为
P(A1+A2)=1-P(A3+A4)=1-P(A3)-P(A4)
=1-
 -
-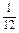 =
= =
=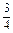 .
.(2)A1+A2+A3的对立事件为A4.
P(A1+A2+A3)=1-P(A4)=1-
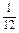 =
=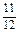 .
.
练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
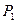 ,机械检查时K=15的概率为
,机械检查时K=15的概率为 ,则有( )
,则有( )
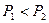

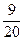 ,则参加联欢会的人数共有 人。
,则参加联欢会的人数共有 人。