题目内容
某企业的某种产品产量与单位成本统计数据如下:
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 产量(千克) | 2 | 3 | 4 | 3 | 4 | 5 |
| 单位成本(元/件) | 73 | 72 | 71 | 73 | 69 | 68 |
(2)指出产量每增加1000件时,单位成本下降多少?
(3)假定产量为6000件时,单位成本是多少?单位成本为70元/件时,产量应为多少?
(1)设x表示每月产量(单位:千件),y表示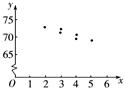
单位成本(单位:元/件),作散点图.由图知y与x间呈线性相关关系,设线性回归方程=x+.
由公式可求得≈-1.818,
=77.363.
∴回归方程为
=-1.818x+77.363.
(2)由回归方程知,每增加1000件产量,单位成本下降1.818元.
(3)当x=6时,=-1.818×6+77.363=66.455;
当=70时,
70=-1.818x+77.363,得x≈4.050千件.
∴产量为6000件时,单位成本是66.455元/件;
单位成本是70元/件时,产量约为4050件.
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
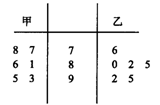
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 | 27 | 38 | 30 | 37 | 35 | 31 |
| 乙 | 33 | 29 | 38 | 34 | 28 | 36 |
(本题满分12分)
某高校在2010年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下左图所示.
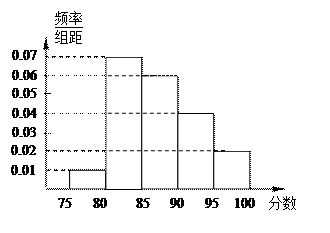
(1)请先求出频率分布表中①、②位置相应的数据,再在答题纸上完成下列频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官进行面试,求第4组至少有一名学生被考官A面试的概率?
| 组号 | 分组 | 频数 | 频率 |
| 第1组 |  | 5 | 0.050 |
| 第2组 |  | ① | 0.350 |
| 第3组 |  | 30 | ② |
| 第4组 |  | 20 | 0.200 |
| 第5组 | 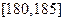 | 10 | 0.100 |
| 合计 | 100 | 1.000 | |
|
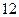 分)
分)
 条道路中抽取
条道路中抽取 条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的
条,它们的得分组成一个样本,求该样本的平均数与总体的平均数之差的 绝对值不超过
绝对值不超过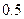 的概率.
的概率.
 人,
人,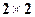 的列联表;
的列联表;