题目内容
若函数f(x)=A.[-
解析:令u=g(x)= 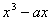 ,y=f(x) 则y=
,y=f(x) 则y= 由题意知 当x∈(-
由题意知 当x∈(-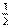 ,0)时,u>0
,0)时,u>0
注意到g(0),故u=g(x)在(- ,0)上为减函数.① 又y=f(x)在(-
,0)上为减函数.① 又y=f(x)在(-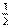 ,0)上为增函数,
,0)上为增函数,
∴y= 在u的相应区间上为减函数. ∴0<a<1
在u的相应区间上为减函数. ∴0<a<1
再由①得u'=g'(x)=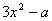 在(-
在(- ,0)上满足u'≤0 ②
,0)上满足u'≤0 ②
而u'=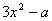 在(-
在(-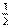 ,0)上为减函数,且是R上的连续函数. ③
,0)上为减函数,且是R上的连续函数. ③
∴由②③得u'(- )≤0 ∴
)≤0 ∴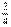 -a≤0,即a≥
-a≤0,即a≥ ④ 于是由①,④得
④ 于是由①,④得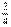 ≤a<1 应选B.
≤a<1 应选B.
注意到g(0),故u=g(x)在(-
∴y=
再由①得u'=g'(x)=
而u'=
∴由②③得u'(-

练习册系列答案
相关题目
若函数f(x)=loga(
)(a>0且a≠1)的定义域和值域都是[0,1],则a=( )
| 1 |
| x+1 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
若函数f ( x )=-
lnx的图象在x=1处的切线l过点( 0 , -
),且l与圆C:x2+y2=1相交,则点(a,b)与圆C的位置关系是( )
| a |
| b |
| 1 |
| b |
| A、点在圆内 | B、点在圆外 |
| C、点在圆上 | D、不能确定 |