题目内容
已知动点P到点F(2,0)的距离与它到直线x=1的距离之比为(1)求动点P的轨迹方程;
(2)设点P的轨迹为曲线C,过点F作互相垂直的两条直线l1、l2,l1交曲线C于A、B两点,l2交曲线C于M、N两点.求证:![]() +
+![]() 为定值.
为定值.
答案:(1)解:设P(x,y),
由题意得![]() =
=![]() |x-1|.
|x-1|.
化简得x2-y2=2.
所以点P的轨迹方程为x2-y2=2.
(2)证明:当直线l1,l2之一与x轴垂直,不妨设l1与x轴垂直,此时A(2, ![]() ),B(2,-
),B(2,- ![]() ),M(-
),M(-![]() ,0),N(
,0),N(![]() ,0),
,0),
![]() ·
·![]() =(0,
=(0,![]() )·(0,-
)·(0,-![]() )=-2,
)=-2,
![]() ·
·![]() =(-
=(-![]() -2,0)·(
-2,0)·(![]() -2,0)=2,
-2,0)=2,
所以![]() +
+![]() =0.
=0.
当直线l1,l2都不与x轴垂直时,
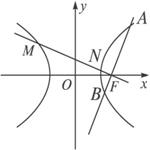
由题意设直线l1为y=k(x-2),k≠0,
则l2的方程为y=![]() (x-2).
(x-2).
由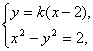 得(1-k2)x2+4k2x-4k2-2=0.
得(1-k2)x2+4k2x-4k2-2=0.
因为l1交双曲线C于A、B两点,
所以
解得k≠±1.
设A(x1,y1),B(x2,y2),
则x1+x2=![]() ,x1x2=
,x1x2=![]() ,y1=k(x1-2),y2=k(x2-2).
,y1=k(x1-2),y2=k(x2-2).
因为![]() =(x1-2,y1),
=(x1-2,y1),![]() =(x2-2,y2),
=(x2-2,y2),
所以![]() ·
·![]() =(x1-2)(x2-2)+y1y2
=(x1-2)(x2-2)+y1y2
=(1+k2)[x1x2-2(x1+x2)+4]
=(1+k2)(![]() +4)
+4)
=![]() .12分
.12分
同理可求得![]() ·
·![]() =
=![]() .
.
所以![]() +
+![]() =
=![]() (
(![]() +
+![]() )=0,
)=0,
即![]() +
+![]() 为定值0.
为定值0.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 .
. =
= ,当点M在直线l上运动时,求点Q的轨迹方程,并说明轨迹是什么曲线.
,当点M在直线l上运动时,求点Q的轨迹方程,并说明轨迹是什么曲线.