题目内容
【题目】已知圆![]() 与直线
与直线![]() 相离,
相离,![]() 是直线
是直线![]() 上任意点,过
上任意点,过![]() 作圆
作圆![]() 的两条切线,切点为
的两条切线,切点为![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)当点![]() 到圆
到圆![]() 的距离最小值为
的距离最小值为![]() 时,证明直线
时,证明直线![]() 过定点.
过定点.
【答案】(1)4;(2)证明见解析.
【解析】
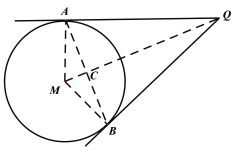
(1) 连接![]() 交于点
交于点![]() ,可求出
,可求出![]() ,从而可求出
,从而可求出![]() ,在直角三角形中,可求出
,在直角三角形中,可求出![]() ,由勾股定理可知
,由勾股定理可知![]() 的长度.
的长度.
(2)由距离最小值可知圆心到直线的距离为![]() ,结合点到直线的距离公式可求出圆心坐标,设
,结合点到直线的距离公式可求出圆心坐标,设![]() ,结合勾股定理可知
,结合勾股定理可知![]() ,从而可求出以
,从而可求出以![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆![]() 的方程,联立圆
的方程,联立圆![]() 与圆
与圆![]() ,整理可得
,整理可得![]() ,令
,令![]() ,即可求出定点的坐标.
,即可求出定点的坐标.
(1)解:连接![]() 交于点
交于点![]() ,由圆的性质可知
,由圆的性质可知![]() ,且
,且![]() ,
,
因为![]() ,所以其半径
,所以其半径![]() ,即
,即![]() ,
,
所以![]() ,则
,则![]() ,
,
所以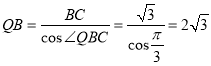 ,则
,则![]()
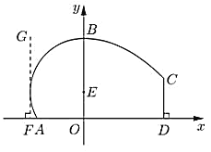
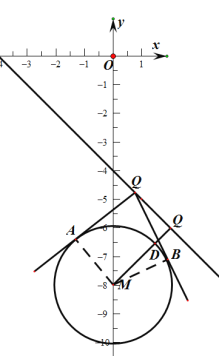
(2)解:过![]() 作直线
作直线![]() 的垂线,当垂足为
的垂线,当垂足为![]() 时,点
时,点![]() 到圆
到圆![]() 的距离最小,
的距离最小,
则![]() ,解得
,解得![]() 或
或![]() (舍去),所以
(舍去),所以![]() ,
,
设![]() ,则
,则![]() ,
,
则以![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆![]() ,
,
则![]() 是圆
是圆![]() 与圆
与圆![]() 的公共弦,则联立得
的公共弦,则联立得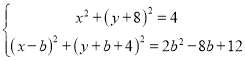 ,
,
两方程相减可得![]() ,令
,令![]() ,解得
,解得![]()
所以直线![]() 过定点
过定点![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目