题目内容
对有10个元素的总体{1,2,3,…,10}进行抽样,先将总体分成两个子总体A={1,2,3,4}和B={5,6,7,8,9,10},再从A和B中分别随机抽取2个元素和3个元素组成样本,用Pij表示元素i和j同时出现在样本中的概率,则P15= , 所有Pij(1≤i<j≤10)的和等于
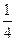 10
10解:(1)由题意有:P15==.
(2)当1≤i<j≤4时,Pij==,这样的Pij共有C个,故所有Pij(1≤i<j≤4)的和为·6=1;
当5≤i<j≤10时,Pij==.
这样的Pij共有C=15个,故所有Pij(5≤i<j≤10)的和为·15=3;
当1≤i≤4,5≤j≤10时,Pij=,这样的Pij共有4·6=24,
所有Pij(1≤i≤4,5≤j≤10)的和为24·=6,
综上所述,所有Pij(1≤i<j≤10)的和等于1+3+6=10.
(2)当1≤i<j≤4时,Pij==,这样的Pij共有C个,故所有Pij(1≤i<j≤4)的和为·6=1;
当5≤i<j≤10时,Pij==.
这样的Pij共有C=15个,故所有Pij(5≤i<j≤10)的和为·15=3;
当1≤i≤4,5≤j≤10时,Pij=,这样的Pij共有4·6=24,
所有Pij(1≤i≤4,5≤j≤10)的和为24·=6,
综上所述,所有Pij(1≤i<j≤10)的和等于1+3+6=10.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
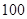 人,不到
人,不到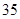 岁的有
岁的有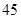 人,
人,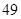 岁的
岁的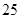 人,剩下的为
人,剩下的为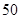 岁以上的人,现在抽取
岁以上的人,现在抽取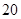 人进行分层抽样,各年龄段人数分别是
人进行分层抽样,各年龄段人数分别是
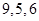
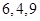
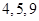
 病人,乙类医院有
病人,乙类医院有 病人,丙类医院有
病人,丙类医院有 病人,为调查三类医院的服务态度,利用分层抽样的方法抽取
病人,为调查三类医院的服务态度,利用分层抽样的方法抽取 人进行调查,则从乙类医院抽取的人数为
人进行调查,则从乙类医院抽取的人数为 人.
人.