题目内容
已知等比数列的前n项和Sn=4n+a,则a的值等于( )
分析:由an=
,利用Sn=4n+a,能求出a1,a2,a3,再由等比数列的性质能求出a的值.
|
解答:解:∵等比数列的前n项和Sn=4n+a,
∴a1= S1=4+a ,
a2=S2-S1=(16+a)-(4+a)=12,
a3=S3-S2=(64+a)-(16+a)=48,
∴122=48(4+a),
解得a=-1.
故选B.
∴a1= S1=4+a ,
a2=S2-S1=(16+a)-(4+a)=12,
a3=S3-S2=(64+a)-(16+a)=48,
∴122=48(4+a),
解得a=-1.
故选B.
点评:本题考查公式由an=
的应用和等比数列的性质,是基础题.解题时要认真审题,仔细解答.
|

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
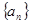 的前n项和为
的前n项和为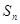 ,且
,且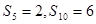 ,则
,则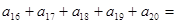 ( )
( )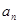 }的前n项和为
}的前n项和为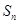 , 满足
, 满足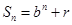 (
(
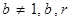 均为常数)
均为常数)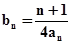
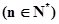 ,求数列
,求数列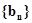 的前
的前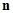 项的和
项的和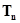 .(6分)
.(6分)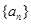 的前n项和为
的前n项和为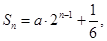 则a的值为( )
则a的值为( )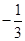 B.
B.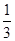 C.
C.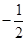 D.
D.