题目内容
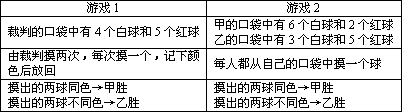
甲、乙两人进行两种游戏,两种游戏的规则由下表给出:(球的大小都相同)| 游戏1 | 游戏2 |
| 裁判的口袋中有4个白球和5个红球 | 甲的口袋中有6个白球和2个红球 乙的口袋中有3个白球和5个红球 |
| 由裁判摸两次,每次摸一个,记下颜色后放回 | 每人都从自己的口袋中摸一个球 |
| 摸出的两球同色→甲胜 摸出的两球不同色→乙胜 | 摸出的两球同色→甲胜 摸出的两球不同色→乙胜 |
(2)求出在游戏2中甲获胜的概率,并说明这两个游戏哪个游戏更公平.
【答案】分析:(1)在游戏1中,每次摸出的球是白球的概率为 ,每次摸出的球是红球的概率为
,每次摸出的球是红球的概率为 ,可得甲获胜的概率为
,可得甲获胜的概率为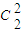 •
•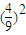 +
+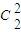 •
•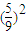 ,用1减去甲获胜的概率即得乙获胜的概率.
,用1减去甲获胜的概率即得乙获胜的概率.
(2)甲乙二人摸出的都是白球的概率为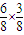 ,甲乙二人摸出的都是红球的概率
,甲乙二人摸出的都是红球的概率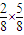 ,把这两个概率相加即得甲胜的概率.比较2个游戏中甲获胜的概率值,概率更接近
,把这两个概率相加即得甲胜的概率.比较2个游戏中甲获胜的概率值,概率更接近 的游戏更公平.
的游戏更公平.
解答:解:(1)在游戏1中,每次摸出的球是白球的概率为 ,每次摸出的球是红球的概率为
,每次摸出的球是红球的概率为 ,
,
故甲获胜的概率为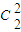 •
•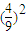 +
+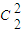 •
•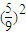 =
=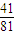 ,乙获胜的概率为1-
,乙获胜的概率为1-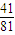 =
=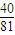 .
.
(2)甲乙二人摸出的都是白球的概率为 =
=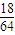 ,甲乙二人摸出的都是红球的概率
,甲乙二人摸出的都是红球的概率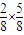 =
=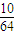 ,
,
故甲胜的概率为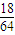 +
+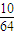 =
=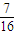 .
.
由于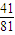 比
比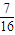 更接近
更接近 ,故游戏1更公平.
,故游戏1更公平.
点评:本题主要考查相互独立事件的概率乘法公式,互斥事件的概率加法公式的应用,所求的事件的概率与它的对立事件的概率之间的关系,属于中档题.
 ,每次摸出的球是红球的概率为
,每次摸出的球是红球的概率为 ,可得甲获胜的概率为
,可得甲获胜的概率为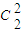 •
•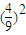 +
+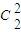 •
•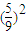 ,用1减去甲获胜的概率即得乙获胜的概率.
,用1减去甲获胜的概率即得乙获胜的概率.(2)甲乙二人摸出的都是白球的概率为
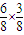 ,甲乙二人摸出的都是红球的概率
,甲乙二人摸出的都是红球的概率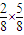 ,把这两个概率相加即得甲胜的概率.比较2个游戏中甲获胜的概率值,概率更接近
,把这两个概率相加即得甲胜的概率.比较2个游戏中甲获胜的概率值,概率更接近 的游戏更公平.
的游戏更公平.解答:解:(1)在游戏1中,每次摸出的球是白球的概率为
 ,每次摸出的球是红球的概率为
,每次摸出的球是红球的概率为 ,
,故甲获胜的概率为
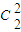 •
•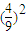 +
+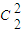 •
•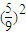 =
=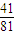 ,乙获胜的概率为1-
,乙获胜的概率为1-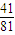 =
=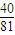 .
.(2)甲乙二人摸出的都是白球的概率为
 =
=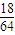 ,甲乙二人摸出的都是红球的概率
,甲乙二人摸出的都是红球的概率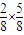 =
=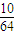 ,
,故甲胜的概率为
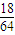 +
+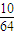 =
=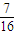 .
.由于
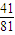 比
比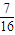 更接近
更接近 ,故游戏1更公平.
,故游戏1更公平.点评:本题主要考查相互独立事件的概率乘法公式,互斥事件的概率加法公式的应用,所求的事件的概率与它的对立事件的概率之间的关系,属于中档题.

练习册系列答案
相关题目