题目内容
给出下列命题:①掷两枚硬币,可出现“两个正面”、“两个反面”、“一正一反”三种等可能结果
②某袋中装有大小均匀的三个红球、两个黑球、一个白球,任取一球,那么每种颜色的球被摸到的可能性不相等;
③分别从3名男同学、4名女同学中各选一名代表,男、女同学当选的可能性相同;
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型.
其中所有错误命题的序号为________.
①③④
分析:①掷两枚硬币,可出现“两个正面”、“两个反面”、“一正一反”三种等可能结果,由可能出现的基本事件数进行判断;
②某袋中装有大小均匀的三个红球、两个黑球、一个白球,任取一球,那么每种颜色的球被摸到的可能性不相等,计算出每种颜色的球被摸到的概率,进行判断;
③分别从3名男同学、4名女同学中各选一名代表,男、女同学当选的可能性相同,计算出男妇同学当选的概率比较大小;
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型,这是一个几何概率模型,由此可以判断.
解答::①不正确,因为掷两枚硬币,可出现“两个正面”、“两个反面”、“一正一反”三种结果,前两种出现的概率是 ,后一种“一正一反”包含两个基本事件,其发生的概率是
,后一种“一正一反”包含两个基本事件,其发生的概率是 ;
;
②是正确命题,因为某袋中装有大小均匀的三个红球、两个黑球、一个白球,任取一球,红球出现的概率是 ,黑球出现的概率是
,黑球出现的概率是 ,白球出现的概率是
,白球出现的概率是 ,故每种颜色的球被摸到的可能性不相等;
,故每种颜色的球被摸到的可能性不相等;
③不正确,因为分别从3名男同学、4名女同学中各选一名代表,男同学当选的概率是 、女同学当选的概率是
、女同学当选的概率是 ,故男女同学当选的可能性不相同;
,故男女同学当选的可能性不相同;
④不正确,因为向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型几何概率樺不是古典概型.
综上知①③④是错误命题
故答案为①③④
点评:本题考查古典概率模型,解题的关键是熟练掌握概率的求法,理解每个命题所涉及的事件,以概率为背景考查命题真假,题型新颖,属于较新的题型
分析:①掷两枚硬币,可出现“两个正面”、“两个反面”、“一正一反”三种等可能结果,由可能出现的基本事件数进行判断;
②某袋中装有大小均匀的三个红球、两个黑球、一个白球,任取一球,那么每种颜色的球被摸到的可能性不相等,计算出每种颜色的球被摸到的概率,进行判断;
③分别从3名男同学、4名女同学中各选一名代表,男、女同学当选的可能性相同,计算出男妇同学当选的概率比较大小;
④向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型是古典概型,这是一个几何概率模型,由此可以判断.
解答::①不正确,因为掷两枚硬币,可出现“两个正面”、“两个反面”、“一正一反”三种结果,前两种出现的概率是
 ,后一种“一正一反”包含两个基本事件,其发生的概率是
,后一种“一正一反”包含两个基本事件,其发生的概率是 ;
;②是正确命题,因为某袋中装有大小均匀的三个红球、两个黑球、一个白球,任取一球,红球出现的概率是
 ,黑球出现的概率是
,黑球出现的概率是 ,白球出现的概率是
,白球出现的概率是 ,故每种颜色的球被摸到的可能性不相等;
,故每种颜色的球被摸到的可能性不相等;③不正确,因为分别从3名男同学、4名女同学中各选一名代表,男同学当选的概率是
 、女同学当选的概率是
、女同学当选的概率是 ,故男女同学当选的可能性不相同;
,故男女同学当选的可能性不相同;④不正确,因为向一个圆面内随机地投一个点,如果该点落在圆内任意一点都是等可能的,则该随机试验的数学模型几何概率樺不是古典概型.
综上知①③④是错误命题
故答案为①③④
点评:本题考查古典概率模型,解题的关键是熟练掌握概率的求法,理解每个命题所涉及的事件,以概率为背景考查命题真假,题型新颖,属于较新的题型

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
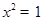 ,则
,则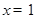 ”的否命题为“若
”的否命题为“若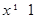 ”;
”;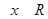 ,
,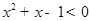 ”的否定是“
”的否定是“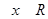 ,
,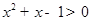 ”;
”;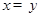 ,则
,则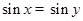 ”的逆否命题为真命题;
”的逆否命题为真命题;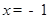 ”是“
”是“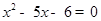 ”的必要不充分条件;
”的必要不充分条件;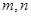 ,则向量
,则向量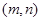 与向量
与向量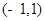 的夹角
的夹角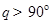 的概率是
的概率是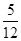 ;
;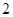 B.
B.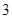 C.
C.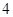 D.
D.