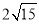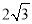题目内容
曲线 是平面内与定点
是平面内与定点 和定直线
和定直线 的距离的积等于
的距离的积等于 的点的轨迹.给出下列四个结论:
的点的轨迹.给出下列四个结论:
①曲线 过坐标原点;
过坐标原点;
②曲线 关于
关于 轴对称;
轴对称;
③曲线 与
与 轴有
轴有 个交点;
个交点;
④若点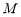 在曲线
在曲线 上,则
上,则 的最小值为
的最小值为 .
.
其中,所有正确结论的序号是___________.
①②④
【解析】
试题分析:设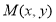 曲线
曲线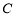 上任意一点,则依题意可得
上任意一点,则依题意可得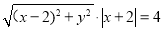 ,将原点代入验证,方程成立,说明曲线
,将原点代入验证,方程成立,说明曲线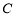 过坐标原点,故①正确;把方程中的x不变,y被-y 代换,方程不变,说明曲线
过坐标原点,故①正确;把方程中的x不变,y被-y 代换,方程不变,说明曲线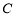 关于
关于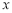 轴对称,故②正确;将
轴对称,故②正确;将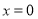 代入方程
代入方程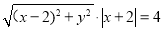 可得
可得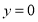 ,即方程只有一个根,所以③不正确;定点
,即方程只有一个根,所以③不正确;定点 和定直线
和定直线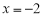 可看做是抛物线
可看做是抛物线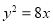 的焦点和准线,设点
的焦点和准线,设点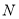 是抛物线上的任意一点,由抛物线的定义可知点
是抛物线上的任意一点,由抛物线的定义可知点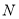 到焦点和准线的距离相等,要使
到焦点和准线的距离相等,要使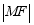 的最小值画图分析可知点
的最小值画图分析可知点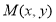 应在抛物线
应在抛物线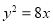 的内侧且
的内侧且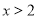 ,当点
,当点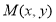 在
在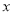 上时
上时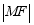 取得最小值,此时
取得最小值,此时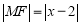 ,点
,点 到直线
到直线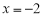 的距离为
的距离为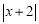 ,所以
,所以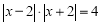 ,解得
,解得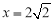 ,此时
,此时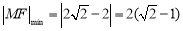 。故④正确。综上可得正确的是①②④。
。故④正确。综上可得正确的是①②④。
考点:1、定义法求轨迹;2、对称问题;3、抛物线的定义;4、数形结合思想和转化思想。

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目