题目内容
下列命题:①若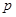 ,
,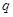 为两个命题,则“
为两个命题,则“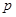 且
且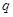 为真”是“
为真”是“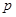 或
或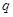 为真”的必要不充分条件。
为真”的必要不充分条件。
②若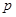 为:
为: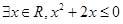 ,则
,则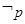 为:
为: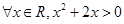 。
。
③命题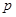 为真命题,命题
为真命题,命题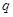 为假命题。则命题
为假命题。则命题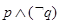 ,
,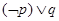 都是真命题。
都是真命题。
④命题“若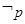 ,则
,则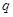 ”的逆否命题是“若
”的逆否命题是“若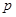 ,则
,则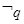 ”. 则正确结论的个数是( )
”. 则正确结论的个数是( )
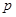 ,
,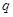 为两个命题,则“
为两个命题,则“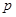 且
且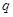 为真”是“
为真”是“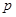 或
或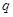 为真”的必要不充分条件。
为真”的必要不充分条件。 ②若
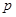 为:
为: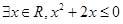 ,则
,则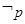 为:
为: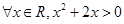 。
。③命题
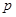 为真命题,命题
为真命题,命题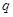 为假命题。则命题
为假命题。则命题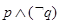 ,
,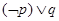 都是真命题。
都是真命题。④命题“若
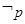 ,则
,则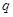 ”的逆否命题是“若
”的逆否命题是“若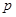 ,则
,则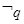 ”. 则正确结论的个数是( )
”. 则正确结论的个数是( )| A.1 | B.2 | C.3 | D.4 |
A
试题分析:命题1中,若
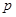 ,
,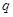 为两个命题,则“
为两个命题,则“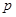 且
且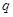 为真”说明都是真命题,而“
为真”说明都是真命题,而“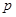 或
或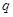 为真”一真即真,那么可见条件是结论的充分不必要条件。故命题1错误。
为真”一真即真,那么可见条件是结论的充分不必要条件。故命题1错误。命题2中,若
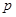 为:
为: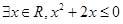 ,则
,则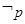 为:
为: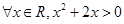 。符合特称命题的否定,成立。
。符合特称命题的否定,成立。命题3中,由于命题 为真命题,命题 为假命题。则命题 ,为真命题,但是 为假命题,因此都是真命题错误。
命题4中,由于根据逆否命题的概念可知命题“若
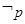 ,则
,则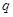 ”的逆否命题是“若
”的逆否命题是“若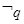 ,则
,则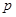 ”.故命题错误,真命题的个数为1个,选A.
”.故命题错误,真命题的个数为1个,选A.点评:解决该试题的关键是能对于复合命题的真值判定理解和运用,同时能根据特称命题和全称命题的关系进行否定得到结论。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
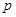 :函数y=1+log
:函数y=1+log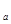 (2x+3)的图像恒过点(-1, 1);命题
(2x+3)的图像恒过点(-1, 1);命题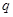 :函数
:函数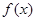 =2sin|x|+1的图像关于y轴对称. 则下列命题:
=2sin|x|+1的图像关于y轴对称. 则下列命题: 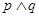 ,
, 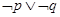 ,
, 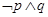 ,
,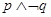 ,
,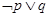 ,
, 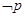 中真命题个数是 .
中真命题个数是 .  :
: , 则
, 则
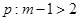 ,命题
,命题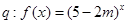 是减函数,
是减函数, 或
或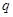 为真命题,
为真命题,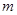 的取值范围.
的取值范围.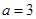 ”是“直线
”是“直线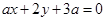 和直线
和直线 平行”的( )
平行”的( )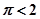 ,Q:
,Q: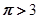 , 则下列判断正确的是( )
, 则下列判断正确的是( ) p”为真
p”为真 ,则
,则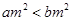 ”的否命题是假命题.
”的否命题是假命题. 为两个不同的平面,直线
为两个不同的平面,直线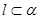 ,则
,则 是
是  成立的充分不必要条件.
成立的充分不必要条件. ”的否定是“
”的否定是“ ”.
”. ,则“
,则“ ”是“
”是“ ”的充分不必要条件.
”的充分不必要条件.