题目内容
在△ABC中,角A、B、C所对的边分别为a,b,c,且
asinB=bcosA.
(I)求角A的大小;
(II)若a=1,且△ABC的面积为
,求b与c的值.
| 3 |
(I)求角A的大小;
(II)若a=1,且△ABC的面积为
| ||
| 4 |
(I)
asinB=bcosA代入正弦定理得:
sinAsinB=sinBcosA,
又0<B<π,得到sinB≠0,所以
sinA=cosA,即tanA=
,
又0<A<π,所以A=
;
(II)∵△ABC的面积为
,即
bcsinA=
,
由(I)得sinA=
,代入得:bc=
①,
由余弦定理a2=b2+c2-2bccosA得:1=b2+c2-3,即b2+c2=4,
所以(b+c)2-2bc=4,(b+c)2=4+2
,所以b+c=1+
②,
由①②解得:
或
.
| 3 |
| 3 |
又0<B<π,得到sinB≠0,所以
| 3 |
| ||
| 3 |
又0<A<π,所以A=
| π |
| 6 |
(II)∵△ABC的面积为
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
由(I)得sinA=
| 1 |
| 2 |
| 3 |
由余弦定理a2=b2+c2-2bccosA得:1=b2+c2-3,即b2+c2=4,
所以(b+c)2-2bc=4,(b+c)2=4+2
| 3 |
| 3 |
由①②解得:
|
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
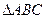
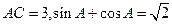
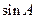 的值;
的值;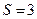 ,求
,求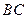 的值
的值
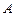 、
、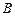 是单位圆
是单位圆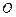 上的动点,
上的动点,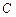 是圆与
是圆与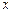 轴正半轴的交点,设
轴正半轴的交点,设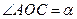 .
.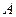 的坐标为
的坐标为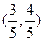 时,求
时,求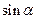 的值;
的值;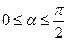 ,且当点A、B在圆上沿逆时针方向移动时总有
,且当点A、B在圆上沿逆时针方向移动时总有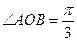 ,试求
,试求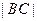 的取值范围.
的取值范围.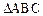 中,化简
中,化简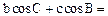 ___________
___________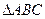 中,
中,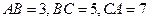 ,则最大边所对的角的大小为___________
,则最大边所对的角的大小为___________