题目内容
如图,在平面四边形 中,
中, ,
,
(1)求 的值;
的值;
(2)求 的长
的长
(1)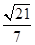 ,(2)
,(2) .
.
解析试题分析:(1)本小题中先在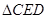 中用余弦定理求得CD,再在
中用余弦定理求得CD,再在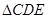 中用正弦定理求得
中用正弦定理求得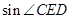 ,注意在用这两个定理时,要找足条件,并正确选择三角形;(2)本小题中
,注意在用这两个定理时,要找足条件,并正确选择三角形;(2)本小题中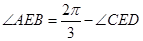 ,而
,而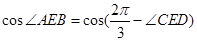 用两角差的余弦公式展开求得,又在
用两角差的余弦公式展开求得,又在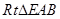 中,
中,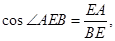 故
故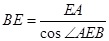 即可求得其值.
即可求得其值.
试题解析:(1)设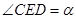 ,在
,在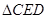 中,由余弦定理,得
中,由余弦定理,得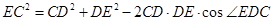 ,于是由题设知,
,于是由题设知,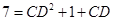 ,即
,即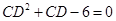 ,解得
,解得 (
(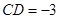 舍去),在
舍去),在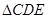 中,由正弦定理,得
中,由正弦定理,得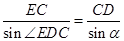 ,于是,
,于是,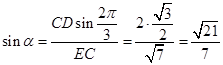 ,即
,即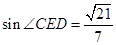 .
.
(2)由题设知,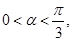 于是由(1)知,
于是由(1)知,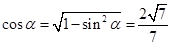 ,而
,而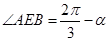 ,所以
,所以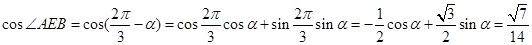 ,在
,在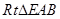 中,
中,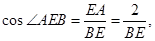 故
故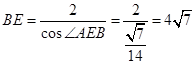 .
.
考点:余弦定理,正弦定理,同角三角函数的基本关系,直角三角形的边角关系,两角差的余弦公式.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
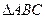 中,
中,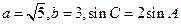
 的长度;
的长度; ,已知石塔的高度为
,已知石塔的高度为 .
. 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点
处测得地面上一点 的俯角为
的俯角为 ,在塔底
,在塔底 处测得
处测得 ,用
,用 表示山的高度
表示山的高度 ;
; 上,其中
上,其中 是塔顶
是塔顶 ,当观测点
,当观测点 在
在 时看
时看 )最大,求山的高度
)最大,求山的高度
 中,
中,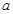 、
、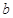 、
、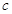 分别为内角
分别为内角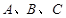 的对边,且
的对边,且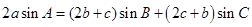 .
. 的大小;(5分)
的大小;(5分)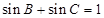 ,判断△
,判断△ 海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距
海里的两个观测点,现位于A点北偏东45°,B点北偏西60°的D点有一艘轮船发出求救信号,位于B点南偏西60°且与B点相距 海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
海里的C点的救援船立即即前往营救,其航行速度为30海里/小时,该救援船到达D点需要多长时间?
 ,
,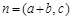 ,且
,且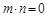
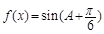 的值域.
的值域. 中,角A,B,C分别所对的边为
中,角A,B,C分别所对的边为 ,且
,且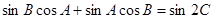 ,
,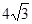 .
. ,求边长
,求边长 .
. 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,满足
,满足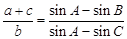 .
.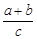 的取值范围.
的取值范围.