题目内容
甲、乙两人独立破译一个密码,他们能独立译出密码的概率分别为| 1 |
| 2 |
| 1 |
| 4 |
(I)求甲、乙两人均不能译出密码的概率;
(II)假设有4个与甲同样能力的人一起独立破译该密码,求这4人中至少有3人同时译出密码的概率.
分析:(I)本题是一个相互独立事件同时发生的概率,根据所给的两个人能够独立的破译密码的概率,做出结果.
(II)有4个与甲同样能力的人一起独立破译该密码,相当于发生四次独立重复试验,成功的概率是
,4人中至少有3人同时译出密码,包括两种情况,这两种情况是互斥的,根据概率公式写出结果.
(II)有4个与甲同样能力的人一起独立破译该密码,相当于发生四次独立重复试验,成功的概率是
| 1 |
| 2 |
解答:解:(I)由题意知本题是一个相互独立事件同时发生的概率,
设“甲、乙两人均不能译出密码”为事件A,
则P(A)=(1-
)(1-
)=
即甲、乙两人均不能译出密码的概率是
(II)有4个与甲同样能力的人一起独立破译该密码,
相当于发生四次独立重复试验,成功的概率是
∴这4人中至少有3人同时译出密码的概率为
(
)3(1-
)+
(
)4=
即这4人中至少有3人同时译出密码的概率为
设“甲、乙两人均不能译出密码”为事件A,
则P(A)=(1-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 8 |
即甲、乙两人均不能译出密码的概率是
| 3 |
| 8 |
(II)有4个与甲同样能力的人一起独立破译该密码,
相当于发生四次独立重复试验,成功的概率是
| 1 |
| 2 |
∴这4人中至少有3人同时译出密码的概率为
| C | 3 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 4 4 |
| 1 |
| 2 |
| 5 |
| 16 |
即这4人中至少有3人同时译出密码的概率为
| 5 |
| 16 |
点评:本题考查相互独立事件同时发生的概率,是一个基础题,本题解题的关键是看出第二问中的事件符合独立重复试验,利用公式求解.

练习册系列答案
相关题目
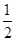 和
和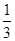 , 求:
, 求: 若甲破译的成功率为
若甲破译的成功率为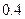 ,乙破译的成功率为
,乙破译的成功率为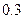 ,则密码破译成功的概率等于
,则密码破译成功的概率等于