题目内容
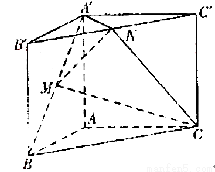
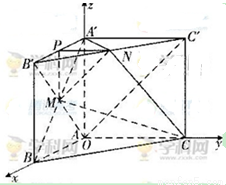
如图,直三棱柱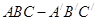 ,
,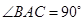 ,
,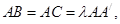 点M,N分别为
点M,N分别为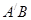 和
和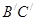 的中点。
的中点。
(Ⅰ)证明: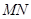 ∥平面
∥平面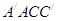 ;
;
(Ⅱ)若二面角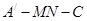 为直二面角,求
为直二面角,求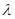 的值。
的值。
【答案】
(1)见解析 (2)
【解析】(1)证法一:连结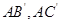 ,由已知
,由已知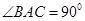
AB=AC,三棱柱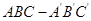 为直三棱柱,所以M为
为直三棱柱,所以M为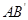 中点,
中点,
又因为N为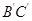 的中点,所以
的中点,所以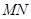 ∥
∥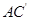 .
.
又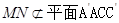 ,
, ,因此
,因此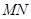 ∥
∥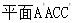
证法二:取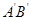 中点P,连结MP,NP,而M,N分别为
中点P,连结MP,NP,而M,N分别为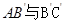 的中点,所以MP∥
的中点,所以MP∥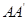 ,PN∥
,PN∥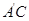 ,所以MP∥
,所以MP∥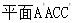 ,PN∥
,PN∥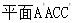 ,又
,又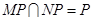 ,
,
因此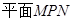 ∥
∥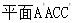 .而
.而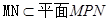 ,因此MN∥
,因此MN∥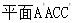
(2)以A为坐标原点,分别以直线AB,AC, 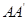 为x轴,y轴,z轴,建立直角坐标系O-xyz,如图所示.
为x轴,y轴,z轴,建立直角坐标系O-xyz,如图所示.
设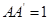 ,则
,则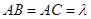 ,
,
于是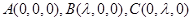 ,
,
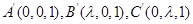 ,
,
所以
设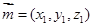 是平面
是平面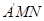 的法向量
的法向量
由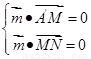 得
得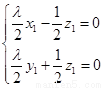
可取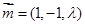
设 是平面
是平面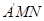 的法向量
的法向量
由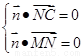 得
得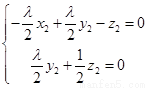
可取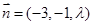
因为 为直二面角,所以
为直二面角,所以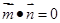
即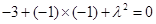 ,解得
,解得
考点定位:本大题主要以直三棱柱为几何背景考查线面垂直的判定和二面角的求法,可以运用传统几何法,也可以用空间向量方法求解.突出考查空间想象能力和计算能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
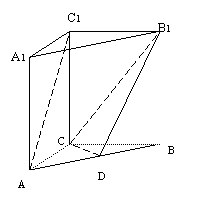
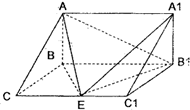 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,E为棱CC1的中点,已知AB=
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,E为棱CC1的中点,已知AB=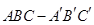 ,
,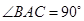 ,
,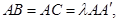 点M,N分别为
点M,N分别为 和
和 的中点.
的中点.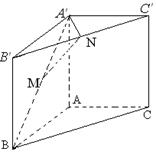
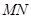 ∥平面
∥平面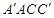 ;
;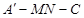 A为直二面角,求
A为直二面角,求 的值.
的值.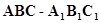 中,
中,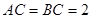 ,
,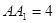 ,
,
 ,点
,点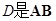 的中点,
的中点,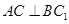
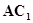 //平面
//平面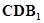 ;
; 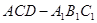 的体积.
的体积.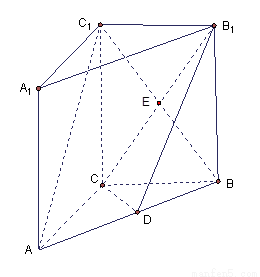
 如图, 在直三棱柱
如图, 在直三棱柱