Question

15．已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右焦点恰为抛物线y²=2px的焦点F，设抛物线的准线l与x轴的交点为M，过F的直线与抛物线交于A，B两点，若以|BM|为直径的圆过点A，则|AB|=（　　）

• A． 2$\sqrt{5}$-2
• B． 4
• C． 2$\sqrt{5}$+2
• D． 4$\sqrt{5}$

Answer 1

分析 如图所示，由椭圆方程可得右焦点F（1，0）．又恰为抛物线y²=2px的焦点F，可得p=2，抛物线方程为：y²=4x．可得M（-1，0）．由题意可知：直线AB的斜率存在且不为0．设直线AB的方程为：y=k（x-1），A（x₁，y₁），B（x₂，y₂）．与抛物线方程联立可得：k²x²-（2k²+4）x+k²=0．解得x_1，2，不妨取x₁=$\frac{{k}^{2}+2-2\sqrt{{k}^{2}+1}}{{k}^{2}}$．x₁+x₂=$\frac{4}{{k}^{2}}$+2．由于AB⊥AM，可得$k•\frac{{y}_{1}-0}{{x}_{1}+1}$=-1，x₁=$\frac{{k}^{2}-1}{{k}^{2}+1}$，解出k²，利用|AB|=x₁+x₂+2=$\frac{4}{{k}^{2}}$+4即可得出．

解答 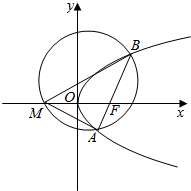解：如图所示，
由椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1可得a=2，b=$\sqrt{3}$，
∴c=$\sqrt{{a}^{2}-{b}^{2}}$=1．
可得右焦点F（1，0）．
又恰为抛物线y²=2px的焦点F，
∴$\frac{p}{2}$=1，解得p=2．
∴抛物线方程为：y²=4x．
可得M（-1，0）．
由题意可知：直线AB的斜率存在且不为0．
设直线AB的方程为：y=k（x-1），A（x₁，y₁），B（x₂，y₂）．
联立$\left\{\begin{array}{l}{y=k（x-1）}\\{{y}^{2}=4x}\end{array}\right.$，化为k²x²-（2k²+4）x+k²=0．
△＞0．
解得x_1，2=$\frac{（{k}^{2}+2）±2\sqrt{{k}^{2}+1}}{{k}^{2}}$，
不妨取x₁=$\frac{{k}^{2}+2-2\sqrt{{k}^{2}+1}}{{k}^{2}}$．
x₁+x₂=$\frac{4}{{k}^{2}}$+2．
∵AB⊥AM，
∴$k•\frac{{y}_{1}-0}{{x}_{1}+1}$=-1，
化为k²（x₁-1）+x₁+1=0，
∴x₁=$\frac{{k}^{2}-1}{{k}^{2}+1}$，
∴$\frac{{k}^{2}-1}{{k}^{2}+1}$=$\frac{{k}^{2}+2-2\sqrt{{k}^{2}+1}}{{k}^{2}}$．
化为k⁴-k²-1=0，
解得k²=$\frac{1+\sqrt{5}}{2}$，
∴|AB|=x₁+x₂+2=$\frac{4}{{k}^{2}}$+4=$\frac{8}{1+\sqrt{5}}+4$=2$\sqrt{5}$+2．
故选：C．

点评 本题考查了椭圆与抛物线的标准方程及其性质、圆的性质、抛物线定义及其弦长公式、相互垂直的直线斜率之间的关系，考查了推理能力与计算能力，属于难题．