题目内容
椭圆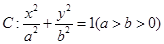 的离心率为
的离心率为 ,两焦点分别为
,两焦点分别为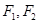 ,点
,点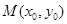 是椭圆C上一点,
是椭圆C上一点,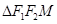 的周长为16,设线段MO(O为坐标原点)与圆
的周长为16,设线段MO(O为坐标原点)与圆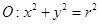 交于点N,且线段MN长度的最小值为
交于点N,且线段MN长度的最小值为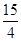 .
.
(1)求椭圆C以及圆O的方程;
(2)当点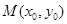 在椭圆C上运动时,判断直线
在椭圆C上运动时,判断直线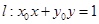 与圆O的位置关系.
与圆O的位置关系.
【答案】
(1)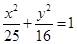
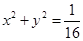
(2)直线l与圆O相交
【解析】
试题分析:解:(1)设椭圆C的半焦距为c,则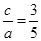 ,即
,即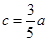 ①
1分
①
1分
又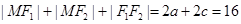 ②
2分
②
2分
联立①②,解得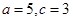 ,所以
,所以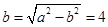 .
.
所以椭圆C的方程为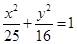 .
4分
.
4分
而椭圆C上点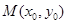 与椭圆中心O的距离为
与椭圆中心O的距离为
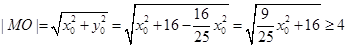 ,等号在
,等号在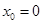 时成立,…6分
时成立,…6分
而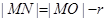 ,则
,则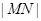 的最小值为
的最小值为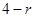 ,从而
,从而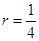 ,则圆O的方程为
,则圆O的方程为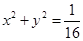 . 8分
. 8分
(2)因为点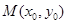 在椭圆C上运动,所以
在椭圆C上运动,所以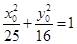 .即
.即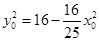 .
.
圆心O到直线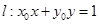 的距离
的距离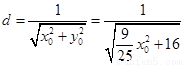 .
11分
.
11分
当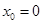 ,
,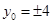 ,
,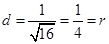 ,则直线l与圆O相切.
,则直线l与圆O相切.
当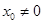 ,
,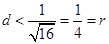 ,则直线l与圆O相交.
14分
,则直线l与圆O相交.
14分
考点:直线与圆的关系,椭圆的方程
点评:主要是考查了椭圆的性质的运用,以及圆的方程,和直线与圆的位置关系,属于基础题。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目


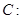
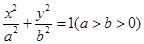 的离心率为
的离心率为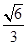 ,椭圆短轴的一个端点与两个焦
,椭圆短轴的一个端点与两个焦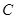 的方程;
的方程;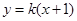 与椭圆
与椭圆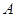 、
、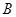 两点. ①若线段
两点. ①若线段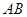 中点的
中点的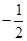 ,求斜率
,求斜率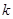 的值;②若点
的值;②若点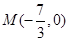 ,求证:
,求证: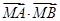 为定值.
为定值.