题目内容

在（x-1）（x-2）（x-3）（x-4）（x-5）的展开式中，含x4的项的系数是________．

-15
分析：本题主要考查二项式定理展开式具体项系数问题．本题可通过选括号（即5个括号中4个提供x，其余1个提供常数）进行求解即可
解答：含x4的项是由（x-1）（x-2）（x-3）（x-4）（x-5）的5个括号中4个括号出x仅1个括号出常数
∴展开式中含x4的项的系数是（-1）+（-2）+（-3）+（-4）+（-5）=-15．
故答案为：-15
点评：本题考查利用分步计数原理和分类加法原理求出特定项的系数．
练习册系列答案
相关题目
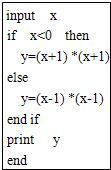精英家教网为了在运行下面的程序之后得到输出y=9，则键盘输入应该是（　　）
input  x
if  x＜0  then
y=（x+1）*（x+1）
else
y=（x-1）*（x-1）
end if
print   y
end
A、x=-4B、x=-2C、x=4或x=-4D、x=2或x=-2
规定Axm=x（x-1）（x-2）•…•（x-m+1），其中x∈R，m∈N*．
函数f（x）=aAx+13+3bAx2+1（ab≠0）在x=1处取得极值，在x=2处的切线的平行向量为
OP
=(b+5，5a)．
（1）求f（x）的解析式；
（2）求f（x）的单调区间；
（3）是否存在正整数m，使得方程f(x)=6x-
16
3
在区间（m，m+1）内有且只有两个不等实根？若存在，求出m的值；若不存在，说明理由．
设函数f（x）是定义在R上的偶函数，且对于任意的x∈R恒有f（x+1）=-f（x），已知当x∈[0，1]时，f（x）=3x．则
①2是f（x）的周期；
②函数f（x）在（2，3）上是增函数；
③函数f（x）的最大值为1，最小值为0；
④直线x=2是函数f（x）图象的一条对称轴．
其中所有正确命题的序号是
①②④
①②④
．
（2009•浦东新区一模）对于函数f1（x），f2（x），h（x），如果存在实数a，b使得h（x）=a•f1（x）+b•f2（x），那么称h（x）为f1（x），f2（x）的生成函数．
（1）下面给出两组函数，h（x）是否分别为f1（x），f2（x）的生成函数？并说明理由．
第一组：f1(x)=sinx，f2(x)=cosx，h(x)=sin(x+
π
3
)；
第二组：f1（x）=x2-x，f2（x）=x2+x+1，h（x）=x2-x+1．
（2）设f1(x)=log2x，f2(x)=log
1
2
x，a=2，b=1，生成函数h（x）．若不等式h（4x）+t•h（2x）＜0在x∈[2，4]上有解，求实数t的取值范围．
（3）设f1(x)=x(x＞0)，f2(x)=
1
x
(x＞0)，取a＞0，b＞0生成函数h（x）图象的最低点坐标为（2，8）．若对于任意正实数x1，x2且x1+x2=1，试问是否存在最大的常数m，使h（x1）h（x2）≥m恒成立？如果存在，求出这个m的值；如果不存在，请说明理由．
在（x-1）（x-2）（x-3）（x-4）（x-5）（x-6）的展开式中，含x5的项的系数是
-21
-21
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网