题目内容
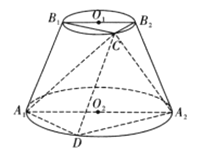
【题目】如图,圆台![]() 的轴截面为等腰梯形
的轴截面为等腰梯形![]() ,
,![]() 圆台
圆台![]() 的侧面积为
的侧面积为![]() .若点
.若点![]() 分别为圆
分别为圆![]() 上的动点,且点
上的动点,且点![]() 在平面
在平面![]() 的同侧.
的同侧.
(1)求证:![]() ;
;
(2)若![]() ,则当三棱锥
,则当三棱锥![]() 的体积取最大值时,求
的体积取最大值时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)根据圆台侧面积公式可以求出上下两底面的半径,根据线面垂直的性质、直角三角形的判断方法进行证明即可;
(2)根据三棱锥的体积公式,结合基本不等式确定![]() 点位置,建立空间直角坐标系,利用空间向量夹角公式进行求解即可.
点位置,建立空间直角坐标系,利用空间向量夹角公式进行求解即可.
(1)证明:设圆![]() 的半径分别为
的半径分别为![]()
因为圆台的侧面积为![]() ,
,
所以![]() ,可得
,可得![]()
因此,在等腰梯形![]() 中,
中,![]() .
.
如图,连接线段![]() ,
,
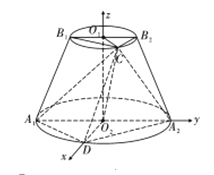
在圆台![]() 中,
中,![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,
,
所以在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() ,
,
故![]() ,即
,即![]() .
.
(2)解:由题意可知,三棱锥![]() 的体积为
的体积为![]()
又在直角三角形中,![]()
所以当且仅当![]() ,
,
即点![]() 为弧
为弧![]() 的中点时,
的中点时,![]() 有最大值
有最大值![]()
连接![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以以![]() 为坐标原点,
为坐标原点,
分别以![]() 的方向为
的方向为![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() .
.
点![]() ,
,
由![]() 可知
可知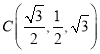 ,
,
![]()

设平面![]() 的法向量
的法向量![]()
则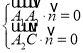 ,
,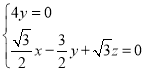 ,
,
取![]() ,
,
则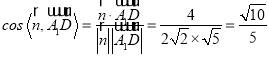
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]()

【题目】保护环境就是保护人类健康.空气中负离子浓度(单位:个/![]() )可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表
)可以作为衡量空气质量的一个指标,也对人的健康有一定的影响.根据我国部分省市区气象部门公布的数据,目前对空气负离子浓度的等级标准如下表![]() .
.
表![]() 负离子浓度与空气质量对应标准:
负离子浓度与空气质量对应标准:
负离子浓度 | 等级 | 和健康的关系 |
|
| 不利 |
|
| 正常 |
|
| 较有利 |
|
| 有利 |
|
| 相当有利 |
|
| 很有利 |
|
| 极有利 |
图![]() 空气负离子浓度
空气负离子浓度
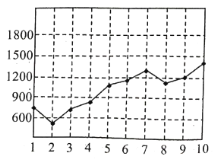
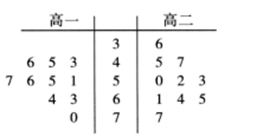
某地连续![]() 天监测了该地空气负离子浓度,并绘制了如图
天监测了该地空气负离子浓度,并绘制了如图![]() 所示的折线图.根据折线图,下列说法错误的是( )
所示的折线图.根据折线图,下列说法错误的是( )
A.这![]() 天的空气负离子浓度总体越来越高
天的空气负离子浓度总体越来越高
B.这![]() 天中空气负离子浓度的中位数约
天中空气负离子浓度的中位数约![]() 个
个![]()
C.后![]() 天的空气质量对身体健康的有利程度明显好于前
天的空气质量对身体健康的有利程度明显好于前![]() 天
天
D.前![]() 天空气质量波动程度小于后
天空气质量波动程度小于后![]() 天
天
【题目】移动支付(支付宝支付,微信支付等)开创了新的支付方式,使电子货币开始普及,为了了解习惯使用移动支付方式是否与年龄有关,对某地200人进行了问卷调查,得到数据如下:60岁以上的人群中,习惯使用移动支付的人数为30人;60岁及以下的人群中,不习惯使用移动支付的人数为40人.已知在全部200人中,随机抽取一人,抽到习惯使用移动支付的人的概率为0.6.
(1)完成如下的列联表,并判断是否有![]() 的把握认为习惯使用移动支付与年龄有关,并说明理由.
的把握认为习惯使用移动支付与年龄有关,并说明理由.
习惯使用移动支付 | 不习惯使用移动支付 | 合计(人数) | |
60岁以上 | |||
60岁及以下 | |||
合计(人数) | 200 |
(2)在习惯使用移动支付的60岁以上的人群中,每月移动支付的金额如下表:
每月支付金额 |
|
|
| 300以上 |
人数 | 10 | 20 |
| 30 |
现采用分层抽样的方法从中抽取9人,再从这9人中随机抽取4人,记4人中每月移动支付金额超过3000元的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |